
 如图,已知AB∥CD,AE∥CF,∠BAE与∠DCF有何关系?说说你的理由.
如图,已知AB∥CD,AE∥CF,∠BAE与∠DCF有何关系?说说你的理由. 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
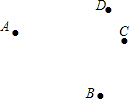 如图,已知平面上有四个点A,B,C,D四个村庄.
如图,已知平面上有四个点A,B,C,D四个村庄.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、2cm,3cm,5cm |
| B、3cm,3cm,6cm |
| C、5cm,8cm,2cm |
| D、4cm,5cm,6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、80m |
| B、45.6m |
| C、40m |
| D、他根本不可能回到出发A点 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,四边形ABCD是一个工件的平面图,它要求AD和BC这两边的夹角应等于30°.甲、乙、丙三个工人在检验工件是否合格时,发生了以下争论:
如图,四边形ABCD是一个工件的平面图,它要求AD和BC这两边的夹角应等于30°.甲、乙、丙三个工人在检验工件是否合格时,发生了以下争论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com