
����Ŀ�����Ķ����в��ϣ�Ȼ�������⣮
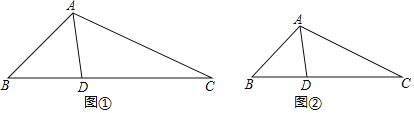
���ϣ��������Σ����ǵ��������Σ�һ����������һ��������Ա��ཻ�������뽻��֮����߶ΰ���������ηָ������С�����Σ�����ֵõ�����С��������һ��Ϊ���������Σ���һ����ԭ���������ƣ����ǰ������߶ν�����������ε������ָ������磺��ͼ����AD�ѡ�ABC�ֳɡ�ABD���ADC������ABD�ǵ��������Σ��ҡ�ADC�ס�BAC����ôAD���ǡ�ABC�������ָ��ߣ�
����������⣺
��1����ͼ�����ڡ�ABC�У���B��40�㣬AD�ǡ�ABC�������ָ��ߣ��ҡ�ABD����ADΪ�ױߵĵ��������Σ����CAD���� ���ȣ�
��2���ڡ�ABC�У���B��42�㣬AD�ǡ�ABC�������ָ��ߣ��ҡ�ABD�ǵ��������Σ����BAC�Ķ�����
���𰸡���1��40����2����BAC�Ķ���Ϊ84���111��
��������
��1�����������ε������ָ��߶������⣻
��2��������������ۣ��������ε������ָ��߶���͵��������ε����ʿ���⣮
�⣺��1����AD�ǡ�ABC�������ָ��ߣ�
���DAC�ס�ABC
���CAD����B��40��
�ʴ�Ϊ��40
��2����BD��AD��
��AD�ǡ�ABC�������ָ��ߣ�
���DAC�ס�ABC
���CAD����B��42��
��AD��BD��
���ABD����BAD��42��
���BAC����BAD+��CAD��84��
��AB��BD��
���BAD��69������BDA
�ߡ�AD�ǡ�ABC�������ָ��ߣ�
���DAC�ס�ABC
���CAD����B��42��
���BAC����BAD+��CAD��42��+69����111��
��AB��AD��
���B����ADB��42��
��AD�ǡ�ABC�������ָ��ߣ�
���DAC�ס�ABC
���CAD����B��42��
�ߡ�ADB����DAC+��C��42��+��C��42��
�����AB��AD��
������������BAC�Ķ���Ϊ84����111��


 ����С״Ԫ��������������ϵ�д�
����С״Ԫ��������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���֪������y��ax2��4amx+3am2��a��mΪ��������a��0��m��0����x�ύ��A��B���㣨A��B����ߣ�����y�ύ�ڵ�C��
��1�����B�����꣨������Ժ�����m����
��2������CA��CB����C��0��3m������tan��ACB��ֵ��
��3����ͼ�ڣ��ڣ�2���������£������ߵĶԳ���Ϊֱ��l��x��2����P���������ϵ�һ�����㣬F�������ߵĶԳ���l�ϵ�һ�㣬�����������Ƿ���ڵ�P��ʹ��POF��Ϊ�Ե�PΪֱ�Ƕ���ĵĵ���ֱ�������Σ������ڣ�������з��������ĵ�P�����꣬�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
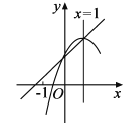
����Ŀ����ͼ��������y��ax2��bx��c(a��0)�Ķ������������y��Ľ�����һ�κ���y��kx��1(k��0)��ͼ���ϣ����ĶԳ�����x��1.�������ĸ����ۣ���. abc��0�� ��. a����![]() ����. a����k����. ��0��x��1ʱ��ax��b��k��������ȷ���۵ĸ�����( )
����. a����k����. ��0��x��1ʱ��ax��b��k��������ȷ���۵ĸ�����( )
A.1��B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
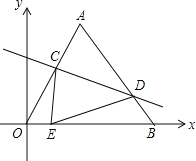
����Ŀ����ͼ����ϵ�У�O��0��0����A��6��6![]() ����B��12��0��������OAB��ֱ��CD�۵���ʹ��Aǡ�������߶�OB�ϵĵ�E������OE��
����B��12��0��������OAB��ֱ��CD�۵���ʹ��Aǡ�������߶�OB�ϵĵ�E������OE��![]() ����AC��AD��ֵ�ǣ�������
����AC��AD��ֵ�ǣ�������
A.1��2B.2��3C.6��7D.7��8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������ɨ�ڳ�����ר���ж�������������һ���������棬���ʱΪ�����ۣ�Ҫ�ھ���ͼ��������Χ����һȦ�ȿ��İױߣ���֪ͼ���ij�Ϊ2�ף���Ϊ1�ף�ͼ�����ռ�����������������90%������ױߵĿ�Ϊx�ף������������г������� ��

A. 90%����2+x����1+x��=2��1 B. 90%����2+2x����1+2x��=2��1
C. 90%����2��2x����1��2x��=2��1 D. ��2+2x����1+2x��=2��1��90%
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
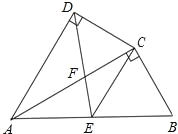
����Ŀ����ͼ���ı���ABCD�У�ACƽ�֡�DAB����ADC����ACB��90�㣬EΪAB���е㣬
��1����֤��AC2��ABAD��
��2����֤����AFD�ס�CFE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y��ax2+bx+c��a��0����ͼ����x�ύ��A��B���㣬��y�ύ��C�㣬�ҶԳ���Ϊx��1����B����Ϊ����1��0������������ĸ����ۣ�������ȷ�ĸ���Ϊ��������
��2a+b��0��4a��2b+c��0��ac��0�ܵ�y��0ʱ����1��x��4
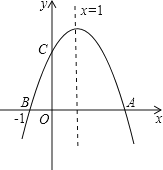
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ��x�ύ�ڵ�A��B����Aλ�ڵ�B����ࣩ����y�ύ�ڵ�C��CD��x�ύ�������ڵ�D��MΪ�����ߵĶ��㣮
��x�ύ�ڵ�A��B����Aλ�ڵ�B����ࣩ����y�ύ�ڵ�C��CD��x�ύ�������ڵ�D��MΪ�����ߵĶ��㣮


��1�����A��B��C�����ꣻ
��2���趯��N����2��n������ʹMN��BN��ֵ��Сʱn��ֵ��
��3��P����������һ�㣬����̽�����Ƿ���ڵ�P��ʹ��P��A��BΪ��������������ABD���ƣ�����PAB���ABD���غϣ��������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������ABC��һ��P�����PAC=��PBA=��PCB�����PΪ��ABC�IJ��忨�㣬�����εIJ��忨���Ƿ�����ѧ�ҳ���ѧ�����ҿ������1816���״η��֣������ķ��ֲ�δ����ʱ��������ע�⣬1875�꣬���忨�㱻һ����ѧ�����߷������ٲ��忨���·��֣�����������������.���⣺��֪�ڵ���ֱ��������DEF�У���EDF=90��������QΪ��DEF�IJ��忨�㣬DQ=1����EQ+FQ=______________ .
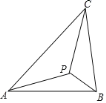
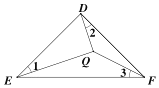
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com