考点:高次方程
专题:计算题
分析:先利用因式分解法解第一个方程得到y=0或y=2,再把第二个方程和第三个方程相减得到4x
2-4z
2=z-x+4zx
2-4xz
2,变形得(x-z)(4x+4z+1-4xz)=0,
所以x-z=0或4x+4z+1-4xz=0,当x=z时,与解①一样得到x=0或x=2,z=0或z=2,即x=y=0或x=z=2;当4x+4z+1-4xz=0,即x=
,把x=
代入第三个方程得4z
2=
(1+4z
2),此方程无解,于是原得到方程组有四组解.
解答:解:
| | 4y2=y(1+4y2)① | | 4x2=z+4zx2② | | 4z2=x+4xz2③ |
| |
,
由①得4y
2-y(1+4y
2)=0,
y(4y-1-4y
2)=0,
y=0或4y-1-4y
2=0,
所以y=0或y=2;
由②-③得4x
2-4z
2=z-x+4zx
2-4xz
2,
4(x+z)(x-z)+(x-z)-4xz(x-z)=0,
(x-z)(4x+4z+1-4xz)=0,
所以x-z=0或4x+4z+1-4xz=0,
当x=z,4x
2=x+4x
3,4z
2=z+4z
3,与解①一样得到x=0或x=2,z=0或z=2,
所以x=y=0或x=z=2,
当4x+4z+1-4xz=0,即x=
,
把x=
代入③得4z
2=
(1+4z
2),
整理得20z
2+4z+1=0,此方程无解,
所以原方程组的解为
或
或
或
.
点评:本题考查了高次方程:整式方程中未知数次数最高项次数高于2次的方程,称为高次方程;高次方程的解法思想:通过适当的方法,把高次方程化为次数较低的方程求解.所以解高次方程一般要降次,即把它转化成二次方程或一次方程.也有的通过因式分解来解.



 快捷英语周周练系列答案
快捷英语周周练系列答案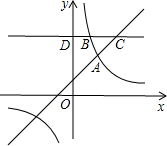 如图,一次函数y=kx+1(k≠0)与反比例函数y=
如图,一次函数y=kx+1(k≠0)与反比例函数y=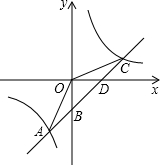 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=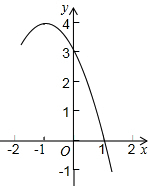 已知抛物线y=-x2+bx-c的部分图象如图所示.
已知抛物线y=-x2+bx-c的部分图象如图所示.