
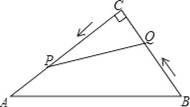
��ͼ����Rt��ACB�У���C=90�㣬AC=30cm��BC=25cm������P�ӵ�C��������CA�����˶����ٶ���2cm/s������Q�ӵ�B��������BC�����˶����ٶ���1cm/s��
��1�������P��Q�������25cm��
��2��������PCQ���ABC���ƣ�
��3�����CPQ�����ΪS1����ABC�����ΪS2�����˶��������Ƿ����ijһʱ��t��ʹ��S1��S2=2��5�������ڣ����t��ֵ���������ڣ���˵�����ɣ�

��
��
�����㡿�������ۺ��⣮
����������1����x���P��Q�������25cm����x��ʾ��CP��CQ�����ݹ��ɶ����г����̣��ⷽ�̼��ɣ�
��2���֡�PCQ�ס�ACB�͡�PCQ�ס�BCA����������������������ε������г���ϵʽ���ⷽ�̼��ɣ�
��3����t�ֱ��ʾ��CP��CQ�����������г����̣��ⷽ�̼��ɣ�
����𡿽⣺��1����x���P��Q�������25cm��
��CP=2xcm��CQ=��25��x��cm��
��������2x��2+��25��x��2=252��
��ã�x1=10��x2=0����ȥ����
��10���P��Q�������25cm��
��2����y����PCQ���ABC���ƣ�
����PCQ�ס�ACBʱ��
 =
=
 ����
����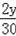
 =
=
 ��
��
��ã�y=
 ��
��
����PCQ�ס�BCAʱ��
 =
=
 ����
����
 =
=
 ��
��
��ã�y=
 ��
��
��
 ���
���
 ����PCQ���ABC���ƣ�
����PCQ���ABC���ƣ�
��3����CPQ�����ΪS1=
 ��CQ��CP=
��CQ��CP=
 ��2t����25��t��=��t2+25t��
��2t����25��t��=��t2+25t��
��ABC�����ΪS2=
 ��AC��BC=375��
��AC��BC=375��
������ã�5����t2+25t��=375��2��
��ã�t1=10��t2=15��
���˶�10���15��ʱ��S1��S2=2��5��
�����������⿼��������������ε��ж��������Լ�һԪ���η��̵�Ӧ�ã��������������ε��ж����������ʶ�������ȷ���һԪ���η����ǽ���Ĺؼ���ע����������˼���Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�����¼��У���Ȼ�¼��ǣ�������
A�����ӣ������ڲ����
B������ö�ʵؾ��ȵ����������ӣ�����֮��һ������6
C���糿��̫���Ӷ�������
D��û��ˮ�֣����ӷ�ѿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪����x��һԪ���η���x2﹣2mx+m2﹣m=o������ʵ����a��b��
��1����ʵ��m��ȡֵ��Χ��
��2�������ʽa2+b2﹣3ab�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��AB��ʾ·�ƣ�������Ϊ1.6��С��վ����·��1.6��D��ʱ��������Լ���·���µ�Ӱ��DE������CD��ȣ���С��������ֱ��BD��ǰ�ߵ�E��ʱ��������ʱС����Ӱ�ӣ��������ʱС����Ӱ����
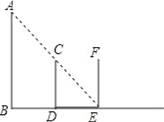

��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��D�ǡ�ABC�ı�AB�ϵ�һ�㣬��ô�����ĸ��������ܵ����ж���ABC�ס�ACD���ǣ�������
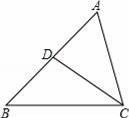

A����B=��ACD B����ADC=��ACB C��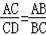
 D��AC2=AD•AB
D��AC2=AD•AB
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����������y=ax2+bx+c��a��0��ͼ���һ���֣���֪�����ߵĶԳ�����x=2����x���һ�������ǣ���1��0���������н��ۣ�
��abc��0��
��4a��2b+c��0��
��4a+b=0��
����������x�����һ�������ǣ�5��0����
�ݵ㣨��3��y1������6��y2�������������ϣ�����y1=y2��
������ȷ���ǣ�������
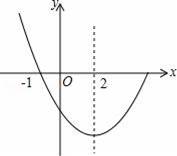

A��4�� B��3�� C��2�� D��1��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���������У�����������ǣ�������
A�����������ζ����� B���ȱ������ζ�����
C����������ζ����� D��ֱ�������ζ�����
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com