
如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动。以CP,CO为邻边构造□PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为 秒.
秒.
(1)当点C运动到线段OB的中点时,求 的值及点E的坐标;
的值及点E的坐标;
(2)当点C在线段OB上时,求证:四边形ADEC为平行四边形;
(3)在线段PE上取点F,使PF=1,过点F作MN⊥PE,截取FM=2,FN=1,且点M,N分别在第一、四象限,在运动过程中,设□PCOD的面积为S.
①当点M,N中,有一点落在四边形ADEC的边上时,求出所有满足条件的 的值;
的值;
②若点M,N中恰好只有一个点落在四边形ADEC内部(不包括边界)时,直接写出S的取值范围.

(1)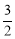 ,(
,( ,0);(2)证明见解析;(3)①1,
,0);(2)证明见解析;(3)①1, ,
,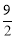 ,5;②
,5;② <S≤
<S≤ 或
或 <S≤20.
<S≤20.
【解析】
试题分析:(1)由C是OB的中点求出时间,再求出点E的坐标.
(2)连接CD交OP于点G,由?PCOD的对角线相等,求四边形ADEC是平行四边形.
(3)①当点C在BO上时,第一种情况,当点M在CE边上时,由△EMF∽△ECO求解,第二种情况,当点N在DE边上时,由△EFN∽△EPD求解,
当点C在BO的延长线上时,第一种情况,当点M在DE边上时,由EMF∽△EDP求解
第二种情况,当点N在CE边上时,由△EFN∽△EOC求解,
②当1≤t< 时和当
时和当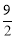 <t≤5时,分别求出S的取值范围,
<t≤5时,分别求出S的取值范围,
当1≤t< 时,S=t(6﹣2t)=﹣2(t﹣
时,S=t(6﹣2t)=﹣2(t﹣ )2+
)2+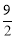 ,
,
∵t= 在1≤t<
在1≤t< 范围内,∴
范围内,∴ <S≤
<S≤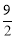 .
.
当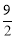 <t≤5时,S=t(2t﹣6)=2(t﹣
<t≤5时,S=t(2t﹣6)=2(t﹣ )2﹣
)2﹣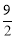 ,∴
,∴ <S≤20.
<S≤20.
试题解析:【解析】
(1)∵OB=6,C是OB的中点,∴BC= OB=3.
OB=3.
∴2t=3,即t=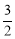 .
.
∴OE= ,E(
,E( ,0).
,0).
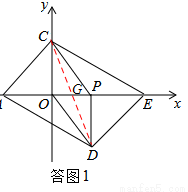
(2)证明:如答图1,连接CD交OP于点G,
在 PCOD中,CG=DG,OG=PG,
PCOD中,CG=DG,OG=PG,
∵AO=PO,∴AG=EG .
∴四边形ADEC是平行四边形.
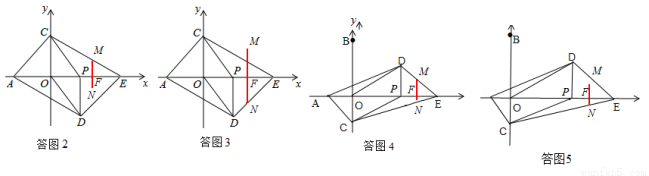
(3)①(Ⅰ)当点C在BO上时,
第一种情况:如答图2,当点M在CE边上时,
∵MF∥OC,∴△EMF∽△ECO.
∴ ,即
,即 ,解得t=1.
,解得t=1.
第二种情况:如答图3,当点N在DE边时,
∵NF∥PD,∴△EFN∽△EPD.
∴ 即
即 ,解得t=
,解得t= .
.
(Ⅱ)当点C在BO的延长线上时,
第一种情况:如答图4,当点M在DE边上时,
∵MF∥PD,∴EMF∽△EDP.
∴ 即
即 ,解得t=
,解得t= .
.
第二种情况:如答图5,当点N在CE边上时,
∵NF∥OC,∴△EFN∽△EOC.
∴ 即
即 ,解得t=5.
,解得t=5.
综上所述,所有满足条件的t的值为1, ,
,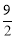 ,5.
,5.
② <S≤
<S≤ 或
或 <S≤20.
<S≤20.
考点:1.双动点问题;2.平行四边形的判定;3.相似三角形的判定和性质;4.二次函数的性质;5.分类思想的应用.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源:2014年初中毕业升学考试(湖北宜昌卷)数学(解析版) 题型:解答题
在“文化宜昌•全民阅读”活动中,某中学社团“精一读书社”对全校学生的人数及纸质图书阅读量(单位:本)进行了调查,2012年全校有1000名学生,2013年全校学生人数比2012年增加10%,2014年全校学生人数比2013年增加100人.
(1)求2014年全校学生人数;
(2)2013年全校学生人均阅读量比2012年多1本,阅读总量比2012年增加1700本(注:阅读总量=人均阅读量×人数)
①求2012年全校学生人均阅读量;
②2012年读书社人均阅读量是全校学生人均阅读量的2.5倍,如果2012年、2014年这两年读书社人均阅读量都比前一年增长一个相同的百分数a,2014年全校学生人均阅读量比2012年增加的百分数也是a,那么2014年读书社全部80名成员的阅读总量将达到全校学生阅读总量的25%,求a的值.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江舟山卷)数学(解析版) 题型:选择题
如图,⊙O的直径CD垂直弦AB于点E,且CE=2,DE=8,则AB的长为( )

(A)2 (B)4 (C)6 (D)8
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江湖州卷)数学(解析版) 题型:填空题
如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江温州卷)数学(解析版) 题型:解答题
一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球、8个黑球、7个红球
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个黑球的概率是 ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江杭州卷)数学(解析版) 题型:解答题
在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P,求证:PB=PC,并请直接写出图中其他相等的线段.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com