
【题目】下表是二次函数y=ax2+bx+c的部分x,y的对应值:
x | … | ﹣1 | ﹣ | 0 |
| 1 |
| 2 |
| 3 | … |
y | … | m |
| ﹣1 |
| ﹣2 |
| ﹣1 |
| 2 | … |
(1)二次函数图象的开口向 ,顶点坐标是 ,m的值为 ;
(2)当x>0时,y的取值范围是 ;
(3)当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时,n的取值范围是 .
【答案】(1)上,(1,-2),2;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由表中所给x、y的对应值,可求得二次函数解析式,然后可得抛物线的开口方向及顶点坐标,令x=1代入可求得m的值;
(2)根据(1)中所求顶点坐标可得答案;
(3)在y=x+n中,将x=1代入可得y=1+n,结合条件可列出关于n的不等式,解不等式可得n的取值范围.
解:(1)把点(0,1),(1,2)和(2,1)代入二次函数解析式,
得: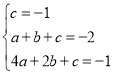 ,解得
,解得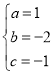 ,
,
∴二次函数解析式为y=x22x1=(x1)22,
∴二次函数图象开口向上,顶点坐标为(1,2),
令x=1,代入y=x22x1可得m=2,
故答案为:上;(1,2);2;
(2)∵顶点坐标为(1,2),
∴当x>0时,y≥2,
故答案为:y≥2;
(3)在y=x+n中,将x=1代入可得y=1+n,
∵抛物线y=ax2+bx+c的顶点在直线y=x+n的下方,
∴1+n>2,解得n>3,
故答案为:n>3.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.

(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;
(2)将图①中的三角板OMN绕点O按逆时针方向旋转,使∠BON=30°,如图③,MN与CD相交于点E,求∠CEN的度数;
(3)将图①中的三角板OMN绕点O按每秒30°的速度按逆时针方向旋转一周,在旋转的过程中,在第____________秒时,直线MN恰好与直线CD垂直.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
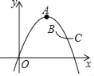
【题目】如图,曲线BC是反比例函数y=![]() (4≤x≤6)的一部分,其中B(4,1﹣m),C(6,﹣m),抛物线y=﹣x2+2bx的顶点记作A.
(4≤x≤6)的一部分,其中B(4,1﹣m),C(6,﹣m),抛物线y=﹣x2+2bx的顶点记作A.
(1)求k的值.
(2)判断点A是否可与点B重合;
(3)若抛物线与BC有交点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
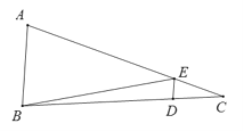
【题目】如图,在△ABC中,D、E分别是BC、AC上的点,且DE∥AB,若S△CDE :S△BDE=1:3,则S△CDE:S△ABE =( )
A.1:9B.1:12
C.1:16D.1:20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:学习了二次根式后,你会发现一些含有根号的式子可以写成另一个式子的平方,如3+2![]() =(1+
=(1+![]() )2,我们来进行以下的探索:
)2,我们来进行以下的探索:
设a+b![]() =(m+n
=(m+n![]() )2(其中a,b,m,n都是正整数),则有a+b
)2(其中a,b,m,n都是正整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() ,∴a=m2+2n2,b=2mn,这样就得出了把类似a+b
,∴a=m2+2n2,b=2mn,这样就得出了把类似a+b![]() 的式子化为平方式的方法,请仿照上述方法探索并解决下列问题:
的式子化为平方式的方法,请仿照上述方法探索并解决下列问题:
(1)当a,b,m,n都为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m,n的式子分别表示a,b,得a= ,b= .
)2,用含m,n的式子分别表示a,b,得a= ,b= .
(2)若a﹣4![]() =(m﹣n
=(m﹣n![]() )2且a,m,n都为正整数,求a的值.
)2且a,m,n都为正整数,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
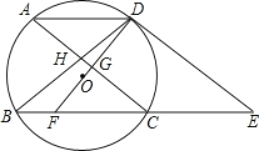
【题目】如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F.
(1)求证:DF垂直平分AC;
(2)求证:FC=CE;
(3)若弦AD=5cm,AC=8cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的y与x的部分对应值如表:
的y与x的部分对应值如表:
x | 1 | 0 | 2 | 3 | 4 |
y | 5 | 0 | 4 | 3 | 0 |
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当0<x<4时,y>0;④抛物线与x轴的两个交点间的距离是4;⑤若A(![]() ,2),B(
,2),B(![]() ,3)是抛物线上两点,则
,3)是抛物线上两点,则![]() ,其中正确的个数是 ( )
,其中正确的个数是 ( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,记千位上和百位上的数字之和为![]() ,十位上和个位上的数字之和为
,十位上和个位上的数字之和为![]() ,如果
,如果![]() ,那么称这个四位数为“和平数”.例如:1423,
,那么称这个四位数为“和平数”.例如:1423,![]() ,
,![]() ,因为
,因为![]() ,所以1423是“和平数”.
,所以1423是“和平数”.
(1)直接写出:最小的“和平数”是_________________,最大的“和平数”是_______________;
(2)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com