
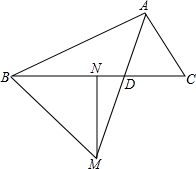
 如图,MN是BC边上的垂直平分线,射线AD交MN于点M,交BC于点D,连接BM.若∠BAM=∠CAM,求证:∠BAM+∠BMN=90°.
如图,MN是BC边上的垂直平分线,射线AD交MN于点M,交BC于点D,连接BM.若∠BAM=∠CAM,求证:∠BAM+∠BMN=90°.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
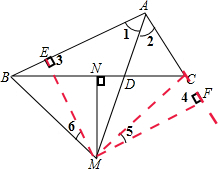 证明:过点M作ME⊥AB,垂足为E,MF⊥AC,垂足为F,连接MC,
证明:过点M作ME⊥AB,垂足为E,MF⊥AC,垂足为F,连接MC,
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
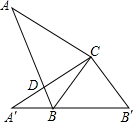 如图,在直角△ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C 的位置,其中A、B′分别是A、B的对应点,且点B在斜边A′B′上,则∠A′CB的度数是
如图,在直角△ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C 的位置,其中A、B′分别是A、B的对应点,且点B在斜边A′B′上,则∠A′CB的度数是查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABCk,∠BAC=90°,∠ABC=65°,△AB1C1由△ABC绕点A顺时针旋转90°得到的(点B1与点B是对应点,点C1与点C是对应点),边接CC1,则∠CC1B1的度数是( )
如图,在Rt△ABCk,∠BAC=90°,∠ABC=65°,△AB1C1由△ABC绕点A顺时针旋转90°得到的(点B1与点B是对应点,点C1与点C是对应点),边接CC1,则∠CC1B1的度数是( )| A、25° | B、20° |
| C、15° | D、10° |
查看答案和解析>>
科目:初中数学 来源: 题型:
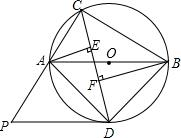 如图,△ABC内接于⊙O,且AB为⊙O的直径,∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.试猜想线段AE、EF、BF之间的关系,并加以证明.
如图,△ABC内接于⊙O,且AB为⊙O的直径,∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.试猜想线段AE、EF、BF之间的关系,并加以证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com