
分析 (1)由一次函数的性质可知函数f(x)=x+1在其值域内单调递增,故不存在峰值;
(2)结合二次函数的性质可知,抛物线的顶点为它的峰值;
(3)结合系数的关系,可将整个x的取值分五段考虑,结合一次函数与二次函数的性质和图象即可得出结论.
解答 解:(1)函数f(x)=x+1在其值域内单调递增,
故函数f(x)=x+1没有峰值.
(2)函数f(x)=x2+4x+1=(x+2)2-3,结合二次函数图象可知:
当x<-2时,函数图形递减;当-2<x时,函数图象递增.
故f(-2)为函数f(x)=x2+4x+1的峰值,
f(-2)=(-2+2)2-3=3,
答:函数f(x)=x2+4x+1的峰值为-3.
(3)根据x-1=0、m=0和m2-1=0,将整个x的取值分五段考虑.
①当m<-1时,即m<0,m2-1>0,
此时图象T1单调递增;图象T2单调递增.
故当m<-1时,图象T所对应的函数f(x)无峰值;
②当m=±1时,图象T2为平行x轴的一条射线,即在此区间f(x)为定值,
故当m=±1时,图象T所对应的函数f(x)无峰值;
③当-1<m<0时,即m<0,m2-1<0,
此时图象T1单调递增;图象T2单调递减.
且当x=m时,y=m(m-1)2+2m2=m3+m;y=(m2-1)m+2m=m3+m,即图象T在m处连续.
故当-1<m<0时,函数f(x)存在峰值f(m).
④当0<m<1时,即m>0,m2-1<0,
此时图象T1单调递减;图象T2单调递减.
故当0<m<1时,图象T所对应的函数f(x)无峰值;
⑤当1<m时,结合二次函数y=m(x-1)2+2m2(x≤m)的图象T1可知:
当x<1时,函数f(x)单调递减;当1<x≤m时,函数f(x)单调递增.
即f(1)是函数f(x)的峰值.
故当1<m时,图象T所对应的函数记为f(x)有峰值f(1).
综上可知:若f(x)存在峰值,实数m的取值范围为-1<m<0或1<m.
点评 本题考查了一次函数和二次函数的性质,解题的关键:(1)一次函数具有单调性;(2)熟悉二次函数的性质;(3)分段考虑,并将一次函数与二次函数性质相结合.本题属于中档题,(1)(2)难度不大,(3)具有一定的难度,主要在于将m分类讨论,失分点在于当-1<m<0时,要得出函数图象T在m处连续.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
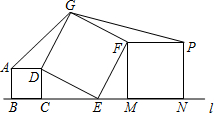 在平面内,按图摆放着三个正方形ABCD、DEFG和MNPF,其中点B、C、E、M、N依次位于直线l上.已知正方形ABCD的面积为4,正方形DEFG的面积为13,则△ADG的面积为$\sqrt{6}$.
在平面内,按图摆放着三个正方形ABCD、DEFG和MNPF,其中点B、C、E、M、N依次位于直线l上.已知正方形ABCD的面积为4,正方形DEFG的面积为13,则△ADG的面积为$\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com