
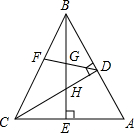
 在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,F为BC中点,BE平分∠ABC,已证△BDH≌△CDA,求证:BG2-GE2=AE2.
在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,F为BC中点,BE平分∠ABC,已证△BDH≌△CDA,求证:BG2-GE2=AE2.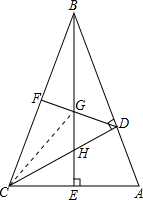
|


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
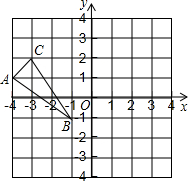 如图,△ABC三个顶点的坐标分别是A(-4,1),B(-1,-1),C(-3,2).
如图,△ABC三个顶点的坐标分别是A(-4,1),B(-1,-1),C(-3,2).查看答案和解析>>
科目:初中数学 来源: 题型:
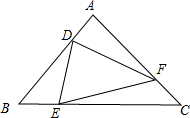 等边△ABC边长为1,D、E、F分别在边AB、BC、CA上,△DEF也是等边三角形.
等边△ABC边长为1,D、E、F分别在边AB、BC、CA上,△DEF也是等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:
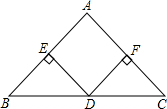 如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F.只添加一个条件,使四边形EDFA是正方形.请你至少写出两种不同的添加方法.并选择一种证明.
如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F.只添加一个条件,使四边形EDFA是正方形.请你至少写出两种不同的添加方法.并选择一种证明.查看答案和解析>>
科目:初中数学 来源: 题型:
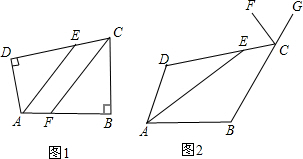 在四边形ABCD中,∠B=∠D=α.
在四边形ABCD中,∠B=∠D=α.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com