
【题目】如图,菱形ABCD的对角线相交于点O,AC=2,BD=2 ![]() ,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为 .
,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为 . 
【答案】7
【解析】解:∵四边形ABCD是菱形,AC=2,BD=2 ![]() , ∴∠ABO=∠CBO,AC⊥BD,
, ∴∠ABO=∠CBO,AC⊥BD,
∵AO=1,BO= ![]() ,
,
∴tan∠ABO= ![]() =
= ![]() ,
,
∴∠ABO=30°,AB=2,
∴∠ABC=60°,
由折叠的性质得,EF⊥BO,OE=BE,∠BEF=∠OEF,
∴BE=BF,EF∥AC,
∴△BEF是等边三角形,
∴∠BEF=60°,
∴∠OEF=60°,
∴∠AEO=60°,
∴△AEO是等边三角形,
∴AE=OE,
∴BE=AE,
∴EF是△ABC的中位线,
∴EF= ![]() AC=1,AE=OE=1,
AC=1,AE=OE=1,
同理CF=OF=1,
∴五边形AEFCD的周长为=1+1+1+2+2=7.
所以答案是:7.
【考点精析】关于本题考查的菱形的性质和翻折变换(折叠问题),需要了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2016次碰到矩形的边时,点P的坐标为( )
A.(0,3)
B.(3,0)
C.(6,4)
D.(1,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两列火车分别从A,B两城同时相向匀速驶出,甲车开往终点B城,乙车开往终点A城,乙车比甲车早到达终点;如图所示,是两车相距的路程d(千米)与行驶时间t(小时)的函数的图象. 
(1)经过小时两车相遇;
(2)A,B两城相距千米路程;
(3)分别求出甲、乙两车的速度;
(4)分别求出甲车距A城的路程s甲、乙车距A城的路程s乙与t的函数关系式;(不必写出t的范围)
(5)当两车相距200千米路程时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,P是对角线AC上任一点(不与A,C重合),连接BP,DP,过P作PE∥CD交AD于E,过P作PF∥AD交CD于F,连接EF. 
(1)求证:△ABP≌△ADP;
(2)若BP=EF,求证:四边形EPFD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过 ![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE. 
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG= ![]() ,AH=3
,AH=3 ![]() ,求EM的值.
,求EM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直. 
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°? (参考数据:sin69°≈ ![]() ,cos21°≈
,cos21°≈ ![]() ,tan20°≈
,tan20°≈ ![]() ,tan43°≈
,tan43°≈ ![]() ,所有结果精确到个位)
,所有结果精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在Rt△ABC中,∠ACB=90°,AC=4,BC=2,D是AC边上的一个动点,将△ABD沿BD所在直线折叠,使点A落在点P处.
(1)如图1,若点D是AC中点,连接PC.
①写出BP,BD的长;
②求证:四边形BCPD是平行四边形.
(2)如图2,若BD=AD,过点P作PH⊥BC交BC的延长线于点H,求PH的长.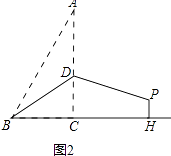
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=﹣ ![]() x+3与坐标轴分别交于点A,B,点P在抛物线y=﹣
x+3与坐标轴分别交于点A,B,点P在抛物线y=﹣ ![]() (x﹣
(x﹣ ![]() )2+4上,能使△ABP为等腰三角形的点P的个数有( )
)2+4上,能使△ABP为等腰三角形的点P的个数有( )
A.3个
B.4个
C.5个
D.6个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com