
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,△COD关于CD的对称图形为△CED.
(1)求证:四边形OCED是菱形;
(2)连接AE,交CD于点M,连接OM,取OM的中点F,连接EF.
①根据题意补全图形;
②若∠ACD=30°,请用等式表示线段CM、DE、EF之间的数量关系,并证明你的结论.
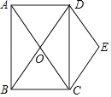
【答案】(1)证明见解析;(2)①见解析;②DE2+CM2=4EF2.证明见解析.
【解析】
(1)根据四边相等的四边形是菱形即可判断.
(2)①根据要求图形即可.
②线段CM、DE、EF之间的数量关系是:DE2+CM2=4EF2.取CM的中点P,连接PF,PE,OE,首先证明四边形AOED是菱形,推出PM是△OCD的中位线,再根据勾股定理即可解决问题.
(1)证明:∵四边形ABCD是矩形,
∴AC与BD相等且互相平分,
∴OC=OD,
∵△COD关于CD的对称图形为△CED,
∴OD=ED,EC=OC,
∴OD=ED=EC=OC,
∴四边形OCED是菱形.
(2)①如图.
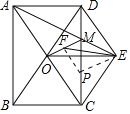
②线段CM、DE、EF之间的数量关系是:DE2+CM2=4EF2.
证明:取CM的中点P,连接PF,PE,OE,
∵四边形ABCD是矩形∴∠ADC=90°
∵∠ACD=30°,
∴∠OAD=∠ADC-∠ACD=60°
∵AO=OD,
∴△AOD是等边三角形,
∴AD=AO,
∵四边形OCED是菱形,
∴DE=OC,∠OCD=∠ECD=30°,OD∥EC,
∴四边形AOED是菱形,
∴AE⊥OD,
∴EN⊥CE,即∠NEC=90°,
∵PM是△OCD的中位线,
∴PF=![]() OC,PF∥OC,
OC,PF∥OC,
∴∠OCD=∠FPM=30°,
∵P是CM的中点,
∴PE=PC=![]() MC,
MC,
∴∠PCE=∠PEC=30°,
∴∠EPM=30°,
∴∠FPE=∠EPM+∠FPM=90°,
根据勾股定理得:PE2+PF2=EF2,
即:(![]() CM)2+(
CM)2+(![]() OC)2=EF2,
OC)2=EF2,
∴DE2+CM2=4EF2.


科目:初中数学 来源: 题型:
【题目】已知:二次函数y=x2+bx+3的图象经过点(3,0).
(1)求b的值;
(2)求出该二次函数图象的顶点坐标和对称轴;
(3)在所给坐标系中画出二次函数y=x2+bx+3的图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
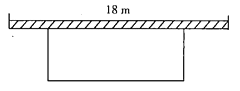
【题目】如图,学校准备在教学楼后面搭建一简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙长为18m),另外三边利用学,校现有总长38m的铁栏围成.
(1)若围成的面积为![]() ,试求出自行车车棚的长和宽;
,试求出自行车车棚的长和宽;
(2)能围成面积为![]() 的自行车车棚吗?如果能,请你给出设计方案;如果不能,请说明理由.
的自行车车棚吗?如果能,请你给出设计方案;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,日销售量y(kg)与时间第t天之间的函数关系式为![]() (
(![]() ,t为整数),销售单价p(元/kg)与时间第t天之间满足一次函数关系如下表:
,t为整数),销售单价p(元/kg)与时间第t天之间满足一次函数关系如下表:
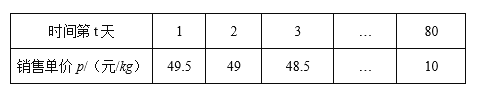
(1)直接写出销售单价p(元/kg)与时间第t天之间的函数关系式.
(2)在整个销售旺季的80天里,哪一天的日销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=10,AD=4,点E从D向C以每秒1个单位的速度运动,以AE为一边在AE的左上方作正方形AEFG,同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动,当点F落在直线MN上,设运动的时间为t,则t的值为( )

A.1B.![]() C.4D.
C.4D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提升学生的艺术素养,某校计划开设四门选修课程:声乐、舞蹈、书法、摄影.要求每名学生必须选修且只能选修一门课程,为保证计划的有效实施,学校随机对部分学生进行了一次调查,并将调査结果绘制成如下不完整的统计表和统计图.
学生选修课程统计表
课程 | 人数 | 所占百分比 |
声乐 | 14 |
|
舞蹈 | 8 |
|
书法 | 16 |
|
摄影 |
|
|
合计 |
|
|

根据以上信息,解答下列问题:
(1)![]() ,
,![]() .
.
(2)求出![]() 的值并补全条形统计图.
的值并补全条形统计图.
(3)该校有1500名学生,请你估计选修“声乐”课程的学生有多少名.
(4)七(1)班和七(2)班各有2人选修“舞蹈”课程且有舞蹈基础,学校准备从这4人中随机抽取2人编排“舞蹈”在开班仪式上表演,请用列表法或画树状图的方法求所抽取的2人恰好来自同一个班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级将举行班级乒乓球对抗赛,每个班必须选派出一对男女混合双打选手参赛.八年级一班准备在小娟、小敏、小华三名女选手和小明、小强两名男选手中,选男、女选手各一名组成一对选手参赛,一共能够组成哪几对?如果小敏和小强的组合是最强组合,那么采用随机抽签的办法,恰好选出小敏和小强参赛的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知在△ABC中,∠B=90°,AB=6cm,BC=12cm,点Q从点A开始沿AB边向点B以1cm/s的速度移动,点P从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果Q、P分别从A、B两点出发,那么几秒后,△PBQ的面积等于8cm2?
(2)在(1)中,△PBQ的面积能否等于10cm2?试说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com