
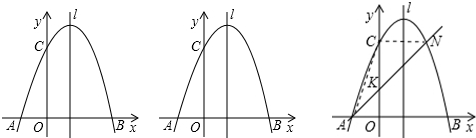
分析 (1)将点的坐标代入抛物线关系式,即可得出结论;
(2)由三角形中两边之和大于第三边可知当△PAC的周长最小时,点P为BC与l的交点;
(3)△MAC为等腰三角形有三种情况,利用两点的距离公式,即可得出结论;
(4)巧妙将△ACN分成两部分,△ACK底为CK,高为1;△NCK底为CK,高为N点横坐标,合在一起底为CK,高为直线AN与抛物线交点的横坐标之差,设出直线解析式,表示出N的横坐标,结合面积公式即可得出结论.
解答 解:(1)∵抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C (0,3)三点,
∴有$\left\{\begin{array}{l}{0=a-b+c}\\{0=9a+3b+c}\\{3=c}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=3}\end{array}\right.$.
即抛物线的函数关系式为y=-x2+2x+3.
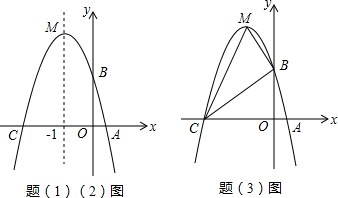
(2)连接PB,如图1.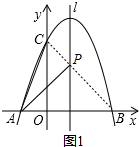
由抛物线的对称性可知PA=PB,
当B、P、C共线时,PB+PC=BC最短(三角形两边之和大于第三边).
∵抛物线的函数关系式为y=-x2+2x+3=-(x-1)2+4,
∴抛物线对称轴l为x=1.
∵B点坐标(3,0)、C点坐标(0,3),
∴直线BC的关系式为y=-x+3.
∵点P为直线l与直线BC的交点,
∴有$\left\{\begin{array}{l}{x=1}\\{y=-x+3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
故当△PAC的周长最小时,点P的坐标为(1,2).
(3)假设存在,设M点的坐标为(1,m),若△MAC为等腰三角形,则有三种情况:
①当CA=CM时,如图2.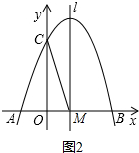
∵A点坐标(-1,0)、C点坐标(0,3),
∴CA=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,CM=$\sqrt{{1}^{2}+(m-3)^{2}}$,
∴$\sqrt{{1}^{2}+(m-3)^{2}}$=$\sqrt{10}$,
解得:m=0.
即M点的坐标为(1,0);
②当MC=MA时,如图3.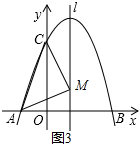
∵MA=$\sqrt{[1-(-1)]^{2}+{m}^{2}}$,MC=$\sqrt{{1}^{2}+(m-3)^{2}}$,
∴$\sqrt{[1-(-1)]^{2}+{m}^{2}}$=$\sqrt{{1}^{2}+(m-3)^{2}}$,
解得:m=1.
即M点的坐标为(1,1);
③当AC=AM时,如图4.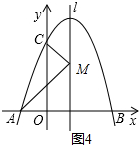
∵AC=$\sqrt{10}$,AM=$\sqrt{[1-(-1)]^{2}+{m}^{2}}$,
∴$\sqrt{10}$=$\sqrt{[1-(-1)]^{2}+{m}^{2}}$,
解得:m=±$\sqrt{6}$.
即M点的坐标为(1,$\sqrt{6}$)或(1,-$\sqrt{6}$).
综上可知:使△MAC为等腰三角形的点M的坐标为(1,0)、(1,1)、(1,$\sqrt{6}$)和(1,-$\sqrt{6}$).
(4)设直线AN的解析式为y=kx+b,则K(0,b).
∵直线AN过点A(-1,0),
∴0=-k+b,即k=b.
直线AN的解析式为y=kx+k.
$\left\{\begin{array}{l}{y=kx+k}\\{y=-{x}^{2}+2x+3}\end{array}\right.$,解得x1=-1,或x2=3-k.
△ACN的面积=$\frac{1}{2}$CK•(x2-x1)=$\frac{1}{2}$(3-k)(4-k)=$\frac{15}{8}$,
解得:k=$\frac{11}{2}$,或k=$\frac{3}{2}$.
∵N点在第一象限呢,
∴x2=3-k>0,即k<3.
∴k=$\frac{11}{2}$不符合,舍去.
故直线AN的解析式为y=$\frac{3}{2}$x+$\frac{3}{2}$.
点评 本题考查了二次函数综合应用的求动点坐标,解题的关键:熟练的运用两点间的距离公式;知道三角形中两边之和大于第三边;以及能找出直线与抛物线交点的问题.本题属于中等难度题,前两问问题不大,(3)的运算量稍微大点,需要用心去做,(4)巧求面积很关键,在直角坐标系中碰到三角形时,经常会以过一个顶点与坐标轴平行的三角形内的线段为底,另两点的横(或纵)坐标之差为高求面积,如想在该类问题中能快速求解需要多练习此类型问题.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段BD、CE交于点M,若AB=AC,AD=AE,则:
如图,已知点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段BD、CE交于点M,若AB=AC,AD=AE,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
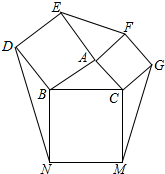 如图,以△ABC的边AB、AC、BC为一边,分别向三角形的外侧作正方形ABDE,正方形ACGF、正方形BCMN
如图,以△ABC的边AB、AC、BC为一边,分别向三角形的外侧作正方形ABDE,正方形ACGF、正方形BCMN查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
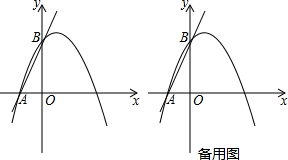
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com