
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 加法交换律 | B. | 加法交换律和加法结合律 | ||
| C. | 加法结合律 | D. | 无法判断 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
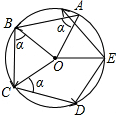 如图,小明从一个圆形场地边沿点A出发,按逆时针方向运动,先沿∠OAB=α的方向走到场地边沿的点B,再沿∠OBC=α的方向走到场地边沿的点C…,照此继续行走并依字母顺序标记,结果点F首次越过了点A并恰好处于$\widehat{AB}$的中点.如果小明希望下一次行走路线正好是⊙O的内接正九边形,那么他应将最初的角α增大或减小多少度?
如图,小明从一个圆形场地边沿点A出发,按逆时针方向运动,先沿∠OAB=α的方向走到场地边沿的点B,再沿∠OBC=α的方向走到场地边沿的点C…,照此继续行走并依字母顺序标记,结果点F首次越过了点A并恰好处于$\widehat{AB}$的中点.如果小明希望下一次行走路线正好是⊙O的内接正九边形,那么他应将最初的角α增大或减小多少度?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com