
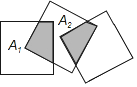
【题目】如图,三个边长均为1的正方形按如图所示的方式摆放,A1,A2分别是正方形对角线的交点,则重叠部分的面积和为______.
【答案】![]()
【解析】
过点A1分别作正方形两边的垂线A1D与A1E,根据正方形的性质可得A1D=A1E,再根据同角的余角相等求出∠BA1D=∠CA1E,然后利用“角边角”证明△A1BD和△A1CE全等,根据全等三角形的面积相等求出阴影部分的面积等于正方形面积的![]() ,即可求解.
,即可求解.
如图,过点A1分别作正方形两边的垂线A1D与A1E,
∵点A1是正方形的中心,
∴A1D=A1E,
∵∠BA1D+∠BA1E=90°,∠CA1E+∠BA1E=90°,
∴∠BA1D=∠CA1E,A1D=A1E,∠A1DB=∠A1EC=90°,
∴△A1BD≌△A1CE(ASA),
∴△A1BD的面积=△A1CE的面积,
∴两个正方形的重合面积=![]() 正方形面积=
正方形面积=![]() ,
,
∴重叠部分的面积和为![]() ×2=
×2=![]() .
.
故答案是:![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】已知等腰△ABC的顶角∠A=36°(如图).
(1)请用尺规作图法作底角∠ABC的平分线BD,交AC于点D(保留作图痕迹,不要求写作法);
(2)证明:△ABC∽△BDC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正确的是( )

A. ①②③④ B. ①② C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.

(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD的两条边在坐标轴上,点D与坐标原点O重合,且AD=8,AB=6.如图2,矩形ABCD沿OB方向以每秒1个单位长度的速度运动,同时点P从A点出发也以每秒1个单位长度的速度沿矩形ABCD的边AB经过点B向点C运动,当点P到达点C时,矩形ABCD和点P同时停止运动,设点P的运动时间为t秒.
(1)当t=5时,请直接写出点D、点P的坐标;
(2)当点P在线段AB或线段BC上运动时,求出△PBD的面积S关于t的函数关系式,并写出相应t的取值范围;
(3)点P在线段AB或线段BC上运动时,作PE⊥x轴,垂足为点E,当△PEO与△BCD相似时,求出相应的t值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着教育教学改革的不断深入,应试教育向素质教育转轨的力度不断加大,体育中考已成为初中毕业升学考试的重要内容之一。为了解某市九年级学生中考体育成绩情况,现从中随机抽取部分考生的体育成绩进行调查,并将调查结果绘制如下图表:
2019年中考体育成绩(分数段)统计表 | ||
分数段 | 频数(人) | 频率 |
25≤x<30 | 12 | 0.05 |
30≤x<35 | 24 | b |
35≤x<40 | 60 | 0.25 |
40≤x<45 | a | 0.45 |
45≤x<50 | 36 | 0.15 |
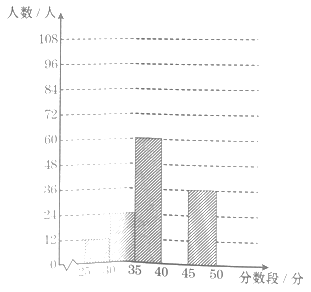
根据上面提供的信息,回答下列问题:
(1)表中a和b所表示的数分别为a=______,b=______;并补全频数分布直方图;
(2)甲同学说“我的体育成绩是此次抽样调查所得数据的中位数。”请问:甲同学的体育成绩在______分数段内?
(3)如果把成绩在40分以上(含40分)定为优秀那么该市12000名九年级考生中考体育成绩为优秀的约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,在平面直角坐标系中,直线y=![]() x-3与坐标轴交于A,B两点.
x-3与坐标轴交于A,B两点.
(1)求A,B两点的坐标;
(2)以AB为边在第四象限内作等边三角形ABC,求△ABC的面积;
(3)在平面内是否存在点M,使得以M,O,A,B为顶点的四边形是平行四边形,若存在,直接写出M点的坐标:若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是昌平区2019年1月份每天的最低和最高气温,观察此图,下列说法正确的是( )

A.在1月份中,最高气温为10℃,最低气温为-2℃
B.在10号至16号的气温中,每天温差最小为7℃
C.每天的最高气温均高于0℃,最低气温均低于0℃
D.每天的最高气温与最低气温都是具有相反意义的量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=24厘米,BC=10厘米,点P从A开始沿AB边以4厘米/秒的速度运动,点Q从C开始沿CD边2厘米/秒的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t秒.
(1)当t=2秒时,求P、Q两点之间的距离;
(2)t为何值时,线段AQ与DP互相平分?
(3)t为何值时,四边形APQD的面积为矩形面积的![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com