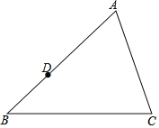
【题目】如图，已知点D为△ABC的边AB上一点
（1）请在边AC上确定一点E，使得S△BCD＝S△BCE（要求：尺规作图、保留作图痕迹、不写作法）；
（2）根据你的作图证明S△BCD＝S△BCE．
名校课堂系列答案科目：初中数学 来源： 题型：
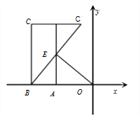
【题目】如图, 已知点A为x轴上的一动点，其坐标为（m，0）点B的坐标为（
，0），在x轴上方取点C，使CB⊥x轴，且CB=2AO，点C，
关于直线
对称，
交直线于点E若△BOE的面积为4，则点E的坐标为________
查看答案和解析>>
科目：初中数学 来源： 题型：
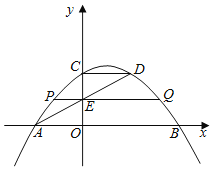
【题目】如图，抛物线y＝﹣
x2+
x+2与x轴相交于A、B两点，与y轴相交于点C，点D在抛物线上，且CD∥AB．AD与y轴相交于点E，过点E的直线PQ平行于x轴，与拋物线相交于P，Q两点，则线段PQ的长为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】脱贫攻坚工作让老百姓过上了幸福的生活．如图①是政府给贫困户新建的房屋，如图②是房屋的侧面示意图，它是一个轴对称图形，对称轴是房屋的高
所在的直线．为了测量房屋的高度，在地面上
点测得屋顶
的仰角为
，此时地面上点、屋檐上
点、屋顶上点三点恰好共线，继续向房屋方向走
到达点
时，又测得屋檐点的仰角为
，房屋的顶层横梁
，
，交
于点
（点，，
在同一水平线上）．（参考数据：
，
，
，
）
（1）求屋顶到横梁的距离
；
（2）求房屋的高（结果精确到
）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．
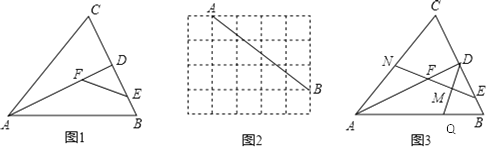
（1）如图1，在△ABC中，AB=AC，AD是△ABC的角平分线，E，F分别是BD，AD上的点．求证：四边形ABEF是邻余四边形．
（2）如图2，在5×4的方格纸中，A，B在格点上，请画出一个符合条件的邻余四边形ABEF，使AB是邻余线，E，F在格点上．
（3）如图3，在（1）的条件下，取EF中点M，连结DM并延长交AB于点Q，延长EF交AC于点N．若N为AC的中点，DE=2BE，QB=6，求邻余线AB的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：对角线互相垂直且相等的四边形叫做垂等四边形．
（1）下面四边形是垂等四边形的是____________（填序号）
①平行四边形；②矩形；③菱形；④正方形
（2）图形判定：如图1，在四边形
中，
∥
，
，过点D作BD垂线交BC的延长线于点E，且
，证明：四边形是垂等四边形．
（3）由菱形面积公式易知性质：垂等四边形的面积等于两条对角线乘积的一半．应用：在图2中，面积为24的垂等四边形内接于⊙O中，
．求⊙O的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我市某学校落实立德树人根本任务，构建“五育并举”教育体系，开设了“厨艺、园艺、电工、木工、编织”五大类劳动课程．为了解七年级学生对每类课程的选择情况，随机抽取了七年级若干名学生进行调查（每人只选一类最喜欢的课程），将调查结果绘制成如下两幅不完整的统计图：
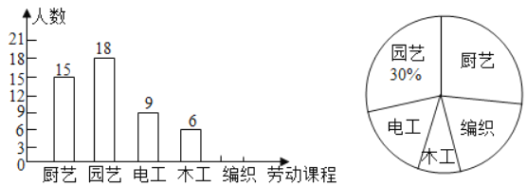
（1）本次随机调查的学生人数为 人；
（2）补全条形统计图；
（3）若该校七年级共有800名学生，请估计该校七年级学生选择“厨艺”劳动课程的人数；
（4）七（1）班计划在“园艺、电工、木工、编织”四大类劳动课程中任选两类参加学校期末展示活动，请用列表或画树状图的方法，求恰好选中“园艺、编织”这两类劳动课程的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】图1是一个地铁站入口的双翼闸机．如图2，它的双翼展开时，双翼边缘的端点A与B之间的距离为10cm，双翼的边缘AC＝BD＝54cm，且与闸机侧立面夹角∠PCA＝∠BDQ＝30°．当双翼收起时，可以通过闸机的物体的最大宽度为( )
A. (54
+10) cm B. (54
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某班男生分成甲、乙两组进行引体向上的专项训练，已知甲组有
名男生，并对两组男生训练前、后引体向上的个数进行统计分析，得到乙组男生训练前、后引体向上的平均个数分别是个和
个，及下面不完整的统计表和统计图．
甲组男生训练前、后引体向上个数统计表（单位：个）
甲组 | 男生 | 男生 | 男生 | 男生 | 男生 | 男生 | 平均个数 | 众数 | 中位数 |
训练前 |
|
|
|
|
|
|
|
|
|
训练后 |
|
|
|
|
|
|
|
|
|
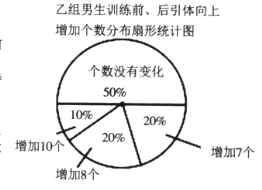
根据以上信息，解答下列问题：
（1）
，
，
；
（2）甲组训练后引体向上的平均个数比训练前增长了 
；
（3）你认为哪组训练效果好？并提供一个支持你观点的理由；
（4）小华说他发现了一个错误：“乙组训练后引体向上个数不变的人数占该组人数的
，所以乙组的平均个数不可能提高
个这么多.”你同意他的观点吗？说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
