练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，直线EF，CD相交于点O，∠AOB=90°，且OD平分∠AOF，∠BOE=2∠AOE，求∠EOD的度数．
    考点：垂线,对顶角、邻补角
    专题：
    分析：利用垂线的定义，以及∠BOE=2∠AOE，得出∠AOE=30°，再利用角平分线的性质得出答案．
    解答：解：∵∠AOB=90°，∠BOE=2∠AOE，
    ∴∠AOE=30°，
    ∴∠AOF=150°，
    ∵OD平分∠AOF，
    ∴∠AOD=75°，
    ∴∠EOD=105°．
    点评：此题主要考查了垂线的定义以及邻补角定义，得出∠AOE的度数是解题关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    小王在一块一边靠墙，长为8米，宽为5米的矩形小花园周围栽种了一种花作修饰，如图所示，这块花园的边框宽为30厘米，内外边框所圈的两个矩形相似吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，△ABC沿DE折叠后，点A落在BC边上的点A′处，且DE∥BC，∠B=50°，则∠BDA′=
     
    度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，是一条高速公路的隧道口在平面直角坐标系上的示意图，点A　和A1、点B和B1分别关于y轴对称，隧道拱部分BCB1为一条抛物线，最高点C离路面AA1的距离为8m，点B离路面为6m，隧道的宽度AA1为16m；
    （1）求图中抛物线对应的函数解析式；
    （2）现有一辆大型运货汽车，装载大型设备后，宽为4m，大型设备与路面距离均为7m，这辆装有大型设备的汽车能否安全通过此隧道？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知函数y=m•xm2+m，m2+m是不大于2的正整数，m取何值时，它的图象开口向上？当x取何值时，y随x的增大而增大？当x取何值时，y随x的增大而减少？当x取何值时，函数有最小值？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    任意△ABC中，∠B=2∠C，∠A、∠B、∠C对应边为a、b、c．求证：b2=c（a+c）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算下列各式，并且把结果化成只含有正整数指数幂的形式：
    （1）（-
    3
    2
    xy）-3÷（
    5
    2
    x2y3）-2；
    （2）（3m2n-2）2•（-4mn-3）-3；
    （3）（
    2
    3
    xy）-2÷（
    1
    3
    x-2）；
    （4）（
    c2
    a2b
    ）2•（
    b2c
    a4
    ）÷（-
    b2
    ca2
    ）-4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    分解因式：60×3.52-120×3.5×1.5+60×1.52．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

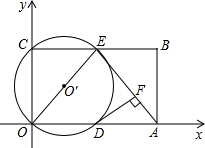    如图，在平面直角坐标系中，矩形ABCO的面积为15，边OA比OC大2．E为BC的中点，以OE为直径的⊙O′交x轴于D点，过点D作DF⊥AE于点F．
    （1）求OA、OC的长；
    （2）求证：DF为⊙O′的切线；
    （3）直线BC上存不存在除点E以外的点P，使△AOP也是等腰三角形？如果不存在，说明理由；如果存在，直接写出P点的坐标．

    查看答案和解析>>

    同步练习册答案