
 如图,正方形ABCD的边长为1,P为BC上任意一点(含B、C两点),分别过点B、C、D作射线AP的垂线,垂足分别为E、F、G,以下判断:
如图,正方形ABCD的边长为1,P为BC上任意一点(含B、C两点),分别过点B、C、D作射线AP的垂线,垂足分别为E、F、G,以下判断:分析 ①利用AAS可证得此结论成立;②令P、C点重合,发现②结论不成立;③④设PB=a,结合三角形面积公式,三角形全等,勾股定理以及相似三角形的性质,用a把BE+CF+DG表示出来,再利用二次函数在a的取值范围内的单调性即可得出结论.
解答 解:①∵∠DAG+∠ADG=90°,∠DAG+∠BAE=90°,
∴∠ADG=∠BAE.
在△ADG和△BAE中,有$\left\{\begin{array}{l}{∠ADG=∠BAE}\\{∠AGD=∠BEA=90°}\\{AD=BA=1}\end{array}\right.$,
∴△ADG≌△BAE(AAS).
故①成立.
②当P在C点时,如图1所示.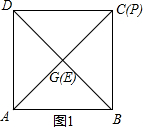
此时,AE=PE=BE=$\frac{\sqrt{2}}{2}$,
显然BE=AE-PE不成立.
故②不成立.
③④放到图2中研究,图2如下.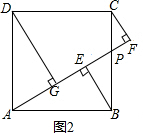
设PB=a(0≤a≤1),则PC=1-a.
由勾股定理可得AP=$\sqrt{A{B}^{2}+P{B}^{2}}$=$\sqrt{1+{a}^{2}}$,
△ABP的面积=$\frac{1}{2}$AP•BE=$\frac{1}{2}$AB•PB,
∴BE=$\frac{a}{\sqrt{1+{a}^{2}}}$.
∵△ADG≌△BAE(①已证),
∴DG=AE.
由勾股定理可得:AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\frac{1}{\sqrt{1+{a}^{2}}}$,
∴DG=$\frac{1}{\sqrt{1+{a}^{2}}}$.
∵∠CPF=∠BPE,∠CFP=∠BEP=90°,
∴△△CFP∽△BEP,
∴$\frac{CF}{BE}$=$\frac{CP}{BP}$,CF=$\frac{CP}{BP}$•BE=$\frac{1-a}{a}$•$\frac{a}{\sqrt{1+{a}^{2}}}$=$\frac{1-a}{\sqrt{1+{a}^{2}}}$.
BE+CF+DG=$\frac{a}{\sqrt{1+{a}^{2}}}$+$\frac{1-a}{\sqrt{1+{a}^{2}}}$+$\frac{1}{\sqrt{1+{a}^{2}}}$=$\frac{2}{\sqrt{1+{a}^{2}}}$.
∵1+a2在0≤a≤1内单调递增,且最小值为1,最大值为2,
∴BE+CF+DG最小值为$\frac{2}{\sqrt{2}}$=$\sqrt{2}$;最大值为$\frac{2}{1}$=2.
故③④成立.
故答案为:①③④.
点评 本题考查了全等三角形的判定及性质、相似三角形的判定及性质、勾股定理以及三角形的面积公式,解题的关键是用a把BE+CF+DG表示出来.本题属于中档题型,难度不大,①②及其容易判定,失分点在于③④的判定,如果像本题一样是填空或者选择,可以考虑特殊点,即P与B或C重合来断定,若为大题,则需设出PB=a,结合三角形面积公式,全等三角形的性质,勾股定理以及相似三角形的性质等众多知识,用a表示出来BE+CF+DG,再用二次函数求最值问题解决问题,结合本题,可以形成一种观念,若为填空、选择直接去找特殊点,这样可以节省很多验证时间.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:选择题
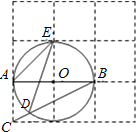 如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的余弦值等于( )
如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的余弦值等于( )| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
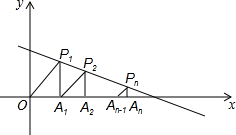 如图所示,在函数y=-$\frac{1}{3}$x+$\frac{4}{3}$(x>0)的图象上,△P1OA,△P2A1A2,△P2A2A3,…,△PnAn-1An都是等腰直角三角形,且直角边OA1,A1A2,…,An-1An都在x轴上,则An的坐标为Pn[1+$\frac{3}{4}$+$\frac{9}{16}$+…($\frac{3}{4}$)n-1,($\frac{3}{4}$)n-1].
如图所示,在函数y=-$\frac{1}{3}$x+$\frac{4}{3}$(x>0)的图象上,△P1OA,△P2A1A2,△P2A2A3,…,△PnAn-1An都是等腰直角三角形,且直角边OA1,A1A2,…,An-1An都在x轴上,则An的坐标为Pn[1+$\frac{3}{4}$+$\frac{9}{16}$+…($\frac{3}{4}$)n-1,($\frac{3}{4}$)n-1].查看答案和解析>>
科目:初中数学 来源: 题型:解答题
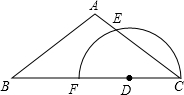 已知:如图,在△ABC中,D是边BC上一点,以点D为圆心,CD为半径作半圆,分别与边AC、BC相交于点E和点F.如果AB=AC=5,cosB=$\frac{4}{5}$,AE=1.求:
已知:如图,在△ABC中,D是边BC上一点,以点D为圆心,CD为半径作半圆,分别与边AC、BC相交于点E和点F.如果AB=AC=5,cosB=$\frac{4}{5}$,AE=1.求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
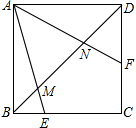 如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=4$\sqrt{2}$,BM=2,则MN的长为$\frac{10}{3}$.
如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=4$\sqrt{2}$,BM=2,则MN的长为$\frac{10}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com