
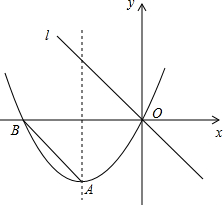
 如图,对称轴为x=-3的抛物线y=ax2+2x 与x 轴相交于点B、O.连结AB,把AB所在的直线平移,使它经过原点O,得到直线l(1)①求抛物线的解析式,并求出顶点A 的坐标;
如图,对称轴为x=-3的抛物线y=ax2+2x 与x 轴相交于点B、O.连结AB,把AB所在的直线平移,使它经过原点O,得到直线l(1)①求抛物线的解析式,并求出顶点A 的坐标;| 1 |
| 3 |
| 1 |
| 3 |
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
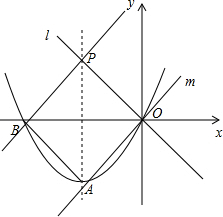 过O、P作直线m、n垂直于直线l;
过O、P作直线m、n垂直于直线l;
|
|
|


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com