
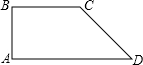
 已知直角梯形上底3cm,下底5cm,另一个底角为45°,建立适当直角坐标系并写出图形中的四个顶点的坐标,求出梯形的面积.
已知直角梯形上底3cm,下底5cm,另一个底角为45°,建立适当直角坐标系并写出图形中的四个顶点的坐标,求出梯形的面积. 分析 在直角梯形ABCD中,AB⊥AD.针对这一特点,可以以线段AD所在的直线为x轴,以线段AB所在的直线为y轴,建立直角坐标系.
解答 解:∵建立直角坐标系如图,A(0,0),作CE⊥AD,垂足为E.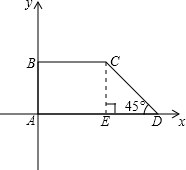 ∵∠EDC=45°,∠CED=90°.
∵∠EDC=45°,∠CED=90°.
∴∠ECD=45°.
∴CE=ED(等角对等边).
∴CE=ED=5-3=2.
∴B(0,2)C(3,2)D(5,0),
梯形的面积=$\frac{1}{2}×(3+5)×2=8c{m}^{2}$.
点评 本题考查了关于坐标系与直角梯形性质的题目,在解答过程中,抓住直角梯形的性质来建坐标系;另外,在解题过程中,也用到三角形的等角对等边的性质.所以,一定要牢记各种图形的性质,这样才避免在解题过程中出现不必要的错误.


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
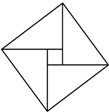 如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是17,小正方形面积是5,直角三角形较长直角边为a,较短直角边为b,则ab的值是( )
如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是17,小正方形面积是5,直角三角形较长直角边为a,较短直角边为b,则ab的值是( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com