
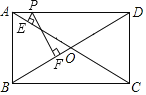
【题目】如图,在矩形ABCD中,AB=15,AD=20,P是AD边上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足为E,F,则PEPF的最大值为_____.

【答案】36.
【解析】
设AP=x,则PD=20﹣x,通过证△APE∽△ACD,△DPF∽△DBA,分别用含x的代数式将PE,PF表示出来,并算出其乘积,然后用二次函数的性质求出其最大值即可.
在Rt△ABD中,BD=![]() =
=![]() =25,
=25,
∵PE⊥AC,PF⊥BD,四边形ABCD是矩形,
∴∠PEA=∠CDA=∠PFD=∠BAD=90°,AC=BD=25,CD=AB=15,
∵∠PAE=∠CAD,∠PEA=∠CDA=90°,
∴△APE∽△ACD,
∴![]() =
=![]() =
=![]() ,
,
∵∠PDF=∠BDA,∠PFD=∠BAD=90°,
∴△DPF∽△DBA,
∴![]() =
=![]() =
=![]() ,
,
设AP=x,则PD=20﹣x,
∴PE=![]() x,PF=
x,PF=![]() (20﹣x)=12﹣
(20﹣x)=12﹣![]() x,
x,
∴PEPF=![]() x×(12﹣
x×(12﹣![]() x)
x)
=﹣![]() x2+
x2+![]() x
x
=﹣![]() (x﹣10)2+36.
(x﹣10)2+36.
∴当x=10时,PEPF有最大值,最大值为36,
故答案为:36


科目:初中数学 来源: 题型:
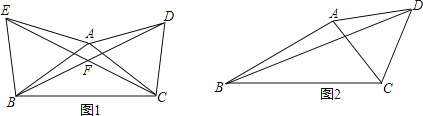
【题目】已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD.
(1)如图1,若AB为边在△ABC外作△ABE,AB=AE,∠DAC=∠EAB=60°,求∠BFC的度数;
(2)如图2,∠ABC=α,∠ACD=β,BC=4,BD=6.
①若α=30°,β=60°,AB的长为 ;
②若改变α、β的大小,且α+β=90°,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)某数学兴趣小组想测量商丘电视台电视塔的高度,如图,该小组在商丘电视塔BC前一座楼房楼顶A处所观测到电视塔最高点B的仰角为65°,电视塔最低点C的仰角为30°,楼顶A与电视塔的水平距离AD为90米,求商丘电视塔BC的高度.(结果精确到1米,参考数据![]() ≈1.41,
≈1.41,![]() ≈1.73,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
≈1.73,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴,垂足为点B,反比例函数y=![]() (x>0)的图象经过AO的中点C,交AB于点D,且AD=3.
(x>0)的图象经过AO的中点C,交AB于点D,且AD=3.
(1)设点A的坐标为(4,4)则点C的坐标为 ;
(2)若点D的坐标为(4,n).
①求反比例函数y=![]() 的表达式;
的表达式;
②求经过C,D两点的直线所对应的函数解析式;
(3)在(2)的条件下,设点E是线段CD上的动点(不与点C,D重合),过点E且平行y轴的直线l与反比例函数的图象交于点F,求△OEF面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
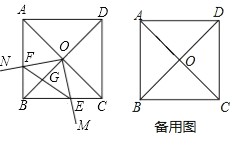
【题目】在正方形ABCD中,AB=8,AC与BD相交于点O.
(1)如图,作射线OM与边BC相交于点E,将射线OM绕点O顺时针旋转90°,得到射线ON,射线ON与边AB相交于点F,连接EF交BO于点G.
①直接写出四边形OEBF的面积是_______.
②求证:△OEF是等腰直角三角形.
③若OG=![]() ,求OE的长.
,求OE的长.
(2)点P在射线CA上一点,若BP=2![]() ,射线PM与直线BC相交于点E,当CE=2时,将射线PM绕点P顺时针旋转45°,得到射线PN,射线PN与直线BC相交于点F,请直接写出BF的长________.
,射线PM与直线BC相交于点E,当CE=2时,将射线PM绕点P顺时针旋转45°,得到射线PN,射线PN与直线BC相交于点F,请直接写出BF的长________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径CD,AB是⊙O的弦,AB⊥CD,垂足为N.连接AC.
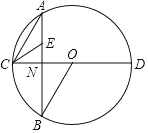
(1)若ON=1,BN=![]() .求弧BC长度;
.求弧BC长度;
(2)若点E在AB上,且AC2=AE.AB.求证:∠CEB=2∠CAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (a≠0)的图象如图所示,则下列命题中正确的是( )
(a≠0)的图象如图所示,则下列命题中正确的是( )

A. a >b>c
B. 一次函数y=ax +c的图象不经第四象限
C. m(am+b)+b<a(m是任意实数)
D. 3b+2c>0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com