
【题目】如图,在△ABC中,∠C=90°,D为AC上的一点,过D作DE⊥AC,过B作BE⊥AB,DE,BE交于点 E.已知BC=3,AB=5.
(1)证明:△EFB∽△ABC.
(2)若CD=1,请求出ED的长.
(3)连结AE,记CD=a,△AFE与△EBF面积的差为b.若存在实数t1,t2,m(其中t1≠t2),当a=t1或a=t2时,b的值都为m.求实数m的取值范围.

【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据相似三角形的判定定理,可求证.(2)过点B作BG⊥ED于G,可得四边形BGDC是矩形,进而可得△EBG∽△ABC,从而求得ED的长.(3)根据△EBG∽△ABC,可得BE,再根据DE∥BC,可得△AFD∽△ABC,即得到AF,从而得到m的取值范围.
解:(1)∵DE⊥AC,BE⊥AB,∠C=90°,
∴DE∥BC,∠EBF=∠ACB=90°,
∴∠EFB=∠ABC,
∴△EFB∽△ABC;
(2)如图,过点B作BG⊥ED于G,

则∠BGE=∠BGD=∠EDC=∠C=90°,
∴四边形BGDC是矩形,
∴BG=CD=1,BC=GD=3,
∵△EFB∽△ABC,
∴∠BEF=∠CAB,
∴△EBG∽△ABC,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
则![]() ;
;
(3)∵CD=a,AC=4,
∴BG=a,AD=4﹣a,
∵△EBG∽△ABC,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
∵DE∥BC,
∴△AFD∽△ABC,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
则![]() ,
,
∴![]()
![]()
![]()
![]() ,
,
∴m的取值范围是![]() .
.


科目:初中数学 来源: 题型:
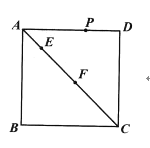
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的两个动点,
上的两个动点,![]() 是正方形四边上的任意一点,且
是正方形四边上的任意一点,且![]() ,设
,设![]() .当
.当![]() 是等腰三角形时,下列关于
是等腰三角形时,下列关于![]() 点个数的说法中,一定正确的是( )
点个数的说法中,一定正确的是( )
①当![]() (即
(即![]() 两点重合)时,
两点重合)时,![]() 点有
点有![]() 个
个
②当![]() 时,
时,![]() 点最多有
点最多有![]() 个
个
③当![]() 点有
点有![]() 个时,x=2
个时,x=2![]() ﹣2
﹣2
④当![]() 是等边三角形时,
是等边三角形时,![]() 点有4个
点有4个
A. ①③B. ①④C. ②④D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种士特产每袋成本10元.试销阶段每袋的销售价x(元)与该士特产的日销售量y(袋)之间的关系如表:
x(元) | 15 | 20 | 30 | … |
y(袋) | 25 | 20 | 10 | … |
若日销售量y是销售价x的一次函数,试求:
(1)日销售量y(袋)与销售价x(元)的函数关系式;
(2)假设后续销售情况与试销阶段效果相同,要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,连接OA,OB,OC,设∠OAC=α,∠OBA=β,∠OCB=γ.则下列叙述中正确的有( )
①若α<β,α<γ,且OC∥AB,则γ=90°﹣α;
②若α:β:γ=1:4:3,则∠ACB=30°;
③若β<α,β<γ,则α+γ﹣β=90°;
④若β<α,β<γ,则∠BAC+∠ABC=α+γ﹣2β.
A. ①②B. ③④C. ①②③D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
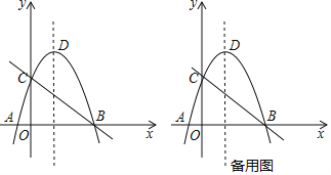
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴另一交点为
轴另一交点为![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线的解析式;
(2)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,求
的值最小,求![]() 的最小值;
的最小值;
(3)在抛物线的对称轴上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.

请你根据统计图解答下列问题:
(1)参加比赛的学生共有____名;
(2)在扇形统计图中,m的值为____,表示“D等级”的扇形的圆心角为____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com