
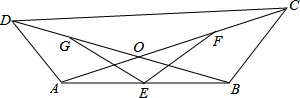
 如图,四边形ABCD的对角线AC、BD相交于点O,E、F、G分别是AB、OC、OD的中点,OA=AD,OB=BC,CD=
如图,四边形ABCD的对角线AC、BD相交于点O,E、F、G分别是AB、OC、OD的中点,OA=AD,OB=BC,CD=| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
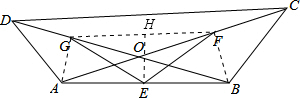 解:连接AG,BF,GF,作EH⊥GF于H,
解:连接AG,BF,GF,作EH⊥GF于H,| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| GH |
| EG |
| ||
| 2 |


科目:初中数学 来源: 题型:
| 测试项目 | 测试成绩(分) | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 75 | 85 | 90 |
| 面试 | 93 | 75 | 72 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,沿AC方向开山修渠,为了加快施工速度,要在小山的另一边同时施工,从AC上的点B取∠ABD=135°,BD=1200米,∠BDE=45°,那么开挖点E离D多远(精确到0.1米),正好能使A、C、E成一条直线.
如图,沿AC方向开山修渠,为了加快施工速度,要在小山的另一边同时施工,从AC上的点B取∠ABD=135°,BD=1200米,∠BDE=45°,那么开挖点E离D多远(精确到0.1米),正好能使A、C、E成一条直线.查看答案和解析>>
科目:初中数学 来源: 题型:
A、0<m<
| ||||
B、0<m<
| ||||
C、0<m<
| ||||
D、0<m<
|
查看答案和解析>>
科目:初中数学 来源: 题型:
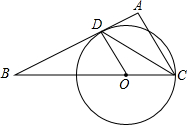 如图,在△ABC中,∠A=90°,CD平分∠ACB交AB于D,AD<AC,过C、D两点做⊙O,且圆心O在BC上.
如图,在△ABC中,∠A=90°,CD平分∠ACB交AB于D,AD<AC,过C、D两点做⊙O,且圆心O在BC上.查看答案和解析>>
科目:初中数学 来源: 题型:
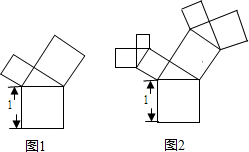 有一个边长为1的正方形,经过一次“生长”后在它的上侧生长出两个小正方形(如图1),且三个正方形所围成的三角形是直角三角形;再经过一次“生长”后变成了图2,如此继续“生长”下去,则“生长”第k次后所有正方形的面积和为( )
有一个边长为1的正方形,经过一次“生长”后在它的上侧生长出两个小正方形(如图1),且三个正方形所围成的三角形是直角三角形;再经过一次“生长”后变成了图2,如此继续“生长”下去,则“生长”第k次后所有正方形的面积和为( )| A、k |
| B、k+1 |
| C、k2 |
| D、(k+1)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,四边形ABCD中,AD∥BC,分别以边AB、CD为一边向四边形ABCD外作正方形ABGE和DCHF,线段AD的垂直平分线交线段AD于点M,交BC于点N.若EP⊥MN于点P,FQ⊥MN于点Q.判断线段EP、FQ的数量关系,并说明理由.(提示:分别过点A,D作PN的平行线)
如图,四边形ABCD中,AD∥BC,分别以边AB、CD为一边向四边形ABCD外作正方形ABGE和DCHF,线段AD的垂直平分线交线段AD于点M,交BC于点N.若EP⊥MN于点P,FQ⊥MN于点Q.判断线段EP、FQ的数量关系,并说明理由.(提示:分别过点A,D作PN的平行线)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com