
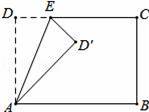
如图,在矩形ABCD中,AD=5,AB=8,点E为DC边上的一个动点,把△ADE沿AE折叠,当点D的对应点刚好D落在矩形ABCD的对称轴上时,则DE的长为 .


 或
或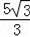
 .
.
【考点】翻折变换(折叠问题).
【分析】过点D′作MN⊥AB于点N,MN交CD于点M,由矩形有两条对称轴可知要分两种情况考虑,根据对称轴的性质以及折叠的特性可找出各边的关系,在直角△EMD′与△AND′中,利用勾股定理可得出关于DM长度的一元二次方程,解方程即可得出结论.
【解答】解:过点D′作MN⊥AB于点N,MN交CD于点M,如图1所示.
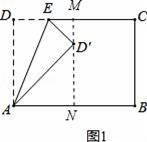

设DE=a,则D′E=a.
∵矩形ABCD有两条对称轴,
∴分两种情况考虑:
①当DM=CM时,
AN=DM=
 CD=
CD=
 AB=4,AD=AD′=5,
AB=4,AD=AD′=5,
由勾股定理可知:
ND′=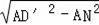
 =3,
=3,
∴MD′=MN﹣ND′=AD﹣ND′=2,EM=DM﹣DE=4﹣a,
∵ED′2=EM2+MD′2,即a2=(4﹣a)2+4,
解得:a=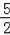
 ;
;
②当MD′=ND′时,
MD′=ND′=
 MN=
MN=
 AD=
AD=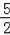
 ,
,
由勾股定理可知:
AN=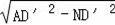
 =
=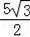
 ,
,
∴EM=DM﹣DE=AN﹣DE=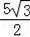
 ﹣a,
﹣a,
∵ED′2=EM2+MD′2,即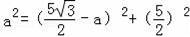
 ,
,
解得:a=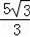
 .
.
综上知:DE=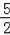
 或
或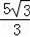
 .
.
故答案为:
 或
或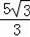
 .
.
【点评】本题考查了翻转变换、轴对称的性质、矩形的性质以及勾股定理,解题的关键是找出关于DM长度的一元二次方程.本题属于中档题,难度不大,但在做题过程中容易丢失一种情况,解决该题型题目时,结合勾股定理列出方程是关键.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
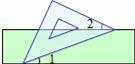

A.30° B.25° C.20° D.15°
查看答案和解析>>
科目:初中数学 来源: 题型:
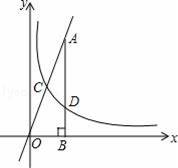
如图,反比例函数y=
 (k≠0,x>0)的图象与直线y=4x相交于点C,过直线上点A(2,8)作AB垂直于x轴于点B,交反比例函数图象于点D,且AD=3BD.
(k≠0,x>0)的图象与直线y=4x相交于点C,过直线上点A(2,8)作AB垂直于x轴于点B,交反比例函数图象于点D,且AD=3BD.
(1)求k的值;
(2)求点C的坐标;
(3)在y轴上是否存在一点P,使点P到C、D两点距离之和PC+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com