
分析 先根据题意得出方程x-1+x-2+x-3+x-4+x-5+x-6+x-7+x-8+x-9+x-10+3x2=(x-1)(x-1-1)+(x-2)(x-2-1)+(x-3)(x-3-1),求出方程的解即可.
解答 解:∵$\sum_{k=1}^{10}{(x-k)}$+3x2=$\sum_{k=1}^3$[(x-k)(x-k-1)],
∴x-1+x-2+x-3+x-4+x-5+x-6+x-7+x-8+x-9+x-10+3x2=(x-1)(x-1-1)+(x-2)(x-2-1)+(x-3)(x-3-1),
10x-55+3x2=x2-3x+2+x2-5x+6+x2-7x+12,
25x=75,
x=3,
故答案为:3.
点评 本题考查了解一元一次方程,整式的混合运算的应用,解此题的关键是能根据题意得出关于x的一元一次方程,有一定的难度.


科目:初中数学 来源: 题型:选择题
| A. | 2004 | B. | 2005 | C. | 2006 | D. | 2007 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
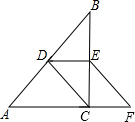 如图,在Rt△ABC中,∠ACB=90°,点D、E分别为AB、BC的中点,点F在AC的延长线上,∠FEC=∠B.请问CF=DE成立吗?试说明理由.(提示:直角三角形斜边上的中线等于斜边的一半.)
如图,在Rt△ABC中,∠ACB=90°,点D、E分别为AB、BC的中点,点F在AC的延长线上,∠FEC=∠B.请问CF=DE成立吗?试说明理由.(提示:直角三角形斜边上的中线等于斜边的一半.)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
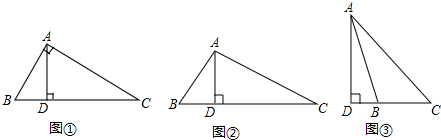
 如图,Rt△ABC中,∠ACB=90°,AC=BC,Rt△DEF中,∠DFE=90°,D、E两点分别在AC、BC上,且DE=BC.若∠CFB=135°,CF=1,EF=3,则AB=5$\sqrt{2}$.
如图,Rt△ABC中,∠ACB=90°,AC=BC,Rt△DEF中,∠DFE=90°,D、E两点分别在AC、BC上,且DE=BC.若∠CFB=135°,CF=1,EF=3,则AB=5$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2010}$ | B. | $\sqrt{2011}$ | C. | $\sqrt{2012}$ | D. | $\sqrt{2013}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com