
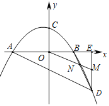
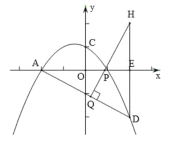
����Ŀ����ͼ�����κ���y��ax2+bx+1��ͼ��x����A����2��0����B��1��0�����㣬��y���ڵ�C����D�ǵ����������������ϵ�һ�����㣬����D��DE��y�ύx���ڵ�E���߶�CB���ӳ��߽�DE�ڵ�M������OM��BD���ڵ�N��
��1������κ����ı���ʽ��
��2����S��OEM��S��DBEʱ�����D�����꼰sin��DAE��ֵ��
��3���ڣ�2���������£���P��x����һ�����㣬��![]() ����Сֵ��
����Сֵ��
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() ����3��
����3��![]()
��������
(1) �ô���ϵ��������![]() ��
��![]() ������������ʽ
������������ʽ![]() ���ɽ��
���ɽ��
(2)�������߿ɵ�BC�������꣬�����ô���ϵ�������ֱ��BC����ʽΪ![]() ����������D����Ϊ��
����������D������![]() ����
����![]() ��
��![]() ����
����![]() �ɵ�OE=DE����
�ɵ�OE=DE����![]() ���������D����Ϊ��2��-2�����������Ǻ�������
���������D����Ϊ��2��-2�����������Ǻ�������![]() �������.
�������.
(3)�ɺ�����ģ�Ϳ�֪������![]() ����
����![]() ת��ΪP�㵽AD�ľ���PQ������D����x��ĶԳƵ�
ת��ΪP�㵽AD�ľ���PQ������D����x��ĶԳƵ�![]() ����H��P��D���㹲����
����H��P��D���㹲����![]() ʱ��
ʱ��![]() ��СֵΪHQ��ֵ������
��СֵΪHQ��ֵ������![]() ���ɼ����
���ɼ����![]() .
.
��1������![]() ��
��![]() ������������ʽ
������������ʽ![]() �У�
�У�
��![]() ���
���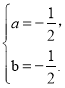
������κ����ı���ʽΪ![]() ��
��
��2����![]() ����
����![]() �ã�
�ã�![]() ����
����![]() ��
��
��ֱ��BC����ʽΪ![]() ������
������![]() ��
��![]() ������������ʽ�У�
������������ʽ�У�
��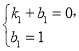 ���
���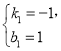
��ֱ��BC�ı���ʽΪ![]() ��
��
��![]() ����
����![]() ��
��![]() ��
��
��![]() ��
��![]() ��BE=x-1��ME=x-1
��BE=x-1��ME=x-1
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() �����
�����![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
��![]() ����
����![]() ��
��
��3����ͼ������D����x��ĶԳƵ�![]() ������P��PQ��AD�ڵ�Q����
������P��PQ��AD�ڵ�Q����![]() ��
��
��![]() ��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
��H��P��D���㹲����![]() ʱ��
ʱ��
![]() ��СֵΪHQ��ֵ��
��СֵΪHQ��ֵ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽����꼶ѧ�������������������������������ȡ�������꼶ѧ����������IJ��Գɼ���Ϊһ����������A��B��C��D�ĸ��ȼ�����ͳ�ƣ��Ƴ�����ͼ��ʾ�IJ�������ͳ��ͼ��
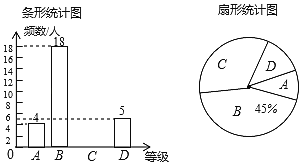
����������Ϣ������������⣺
(1)������ͳ��ͼ�У���ȼ�C��Ӧ������Բ�ĽǵĶ���������ȫ����ͳ��ͼ��
(2)��У���꼶��300��ѧ�������������������Գɼ��ﵽA�ȼ���ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Բ��ΪP��![]() ,
,![]() ���Ķ�Բ������A��1,2������
���Ķ�Բ������A��1,2������![]() �������ڵ�B.
�������ڵ�B.
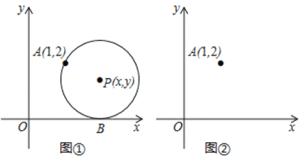
��1����![]() =2�ǣ����P�İ뾶��
=2�ǣ����P�İ뾶��
��2����![]() ����
����![]() �ĺ�������ʽ����ͼ���л����˺���ͼ��
�ĺ�������ʽ����ͼ���л����˺���ͼ��
��3�������Բ�Ķ��壨Բ���Կ����ǵ�����ľ�����ڶ��������е�ļ��ϣ�������2�������ú���ͼ����ж��壺�˺���ͼ����Կ����ǵ� �ľ�����ڵ� �ľ�������е�ļ��ϣ�
��4������P�İ뾶Ϊ1ʱ������P�����ϣ�2�������ú���ͼ���ཻ�ڵ�C��D�����н���D��![]() ��
��![]() ���ڵ�C���Ҳ࣬������ͼ�ڣ���cos��APD= ��
���ڵ�C���Ҳ࣬������ͼ�ڣ���cos��APD= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
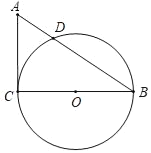
����Ŀ����ͼ����Rt��ACB�У���C��90����AC��3cm��BC��4cm����BCΪֱ������O��AB�ڵ�D��E���߶�AC���е㣬����ED��
��1����֤��ED�ǡ�O���ߣ�
��2�����߶�AD�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��һ�δ�μ��У����������ӻ��ʽ��A���ܲ���B��������C�����٣�D����Ϸ.ȫУѧ����ѡ����һ����ʽ������С�ܶ�ͬѧ��ѡ�õĻ��ʽ����������������飬���ݵ���ͳ�ƽ���������˲�������ͳ��ͼ.


����ͳ��ͼ���ش��������⣺
��1�����ε���ѧ���� �ˣ� ![]() = ����������ͼ����������
= ����������ͼ����������
��2�������У��ѧ��2000�ˣ�������Ƹ�Уѡ�����ܲ������ֻ��ѧ��Լ�ж����ˣ�
��3��ѧУ��ÿ����A��B��C��D���ӻ��ʽ�У������ȡ���ֿ�չ���������״ͼ���б��ķ�������ÿ���ȡ��������ʽǡ�������ܲ��������������ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУֲ����·���������β�����Ƴ����ɸ�ȫ������ͼ����ÿ����һ������ͼ�������γ��Ⱦ�����dcm����ͼ��ʾ����֪ÿ������ͼ���ı߳�Ϊ10![]() cm������һ���ڽ�Ϊ60�㣮
cm������һ���ڽ�Ϊ60�㣮
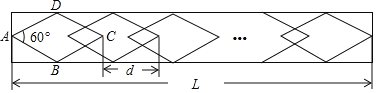
(1)��һ������ͼ��ˮƽ����ĶԽ��߳���
(2)��d��26�����εij���L�ܷ���6010cm�����ܣ�������θ����������ܣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������OA1B1C1�ı߳�Ϊ1����OΪԲ�ģ�OA1Ϊ�뾶������OA1C1����A1C1��OB1�ཻ�ڵ�B2����������OA1B1C1������OA1C1֮�����Ӱ���ֵ����ΪS1��Ȼ����OB2Ϊ�Խ�����������OA2B2C2������OΪԲ�ģ�OA2Ϊ�뾶������OA2C2����A2C2��OB1�ཻ�ڵ�B3����������OA2B2C2������OA2C2֮�����Ӱ�������ΪS2�����˹��ɼ�������ȥ����������OA2018B2018C2018������OA2018C2018֮�����Ӱ�������ΪS2018����S2018��____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����г߹���ͼ�У���ȷ��Բ�ĵ��ǣ�������
����ͼ1����Բ����ȡ������A��B��C���ֱ�����AB��BC�Ĵ�ֱƽ���ߣ�����O��ΪԲ��
����ͼ2����Բ����ȡһ��B����BΪԲ�ģ�С��ֱ����Ϊ�뾶������Բ��A��C��������AB��BC������ABC��ƽ���߽�Բ�ڵ�D������BD�Ĵ�ֱƽ���߽�BD�ڵ�O����O��ΪԲ��
����ͼ3����Բ�Ͻ�ȡ��AB��CD������AB��BC��CD���ֱ�����ABC���DCB��ƽ���ߣ�����O��ΪԲ��

A. �٢�B. �٢�C. �ڢ�D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
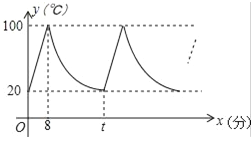
����Ŀ��С������ˮ����ԭ��ˮ���¶�Ϊ20�棬ͨ�翪������ˮ���Զ���ʼ����[�˹�����ˮ��y���棩�뿪��ʱ��x���֣�����һ�κ�����ϵ]�������ȵ�100��ʱ�Զ�ֹͣ���ȣ����ˮ�¿�ʼ�½�[�˹�����ˮ��y���棩�뿪��ʱ��x���֣��ɷ�������ϵ]����ˮ�½���20��ʱ����ˮ�����Զ���ʼ���ȡ����ظ�����������ͼ��ʾ��������ͼ���ṩ����Ϣ������������⣺
��1����0��x��8ʱ����ˮ��y���棩�뿪��ʱ��x���֣��ĺ�����ϵʽ��
��2����ͼ��t��ֵ��
��3����С����ͨ�翪�������ɢ��������Ԥ��С��ɢ��45���ӻص���ʱ����ˮ���ڵ��¶�ԼΪ���١棿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com