
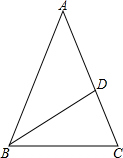
 如图,在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC交AC于D.
如图,在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC交AC于D.| AB |
| BD |
| BC |
| DC |
| 1 |
| x |
| x |
| 1-x |
-1±
| ||
| 2 |
-1+
| ||
| 2 |
-1+
| ||
| 2 |


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
 如图,已知正△ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG=x,设△EFG的面积为y,则y关于x的函数关系式为( )
如图,已知正△ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG=x,设△EFG的面积为y,则y关于x的函数关系式为( )A、-
| ||||||||
B、-
| ||||||||
C、
| ||||||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,PA⊥OA于点A,PB⊥OB于点B,你认为再添加下列哪个条件也不能推出OP垂直平分AB( )
如图,PA⊥OA于点A,PB⊥OB于点B,你认为再添加下列哪个条件也不能推出OP垂直平分AB( )| A、OP⊥AB |
| B、OP平分∠AOB |
| C、PA=PB |
| D、∠OPA=∠OPB |
查看答案和解析>>
科目:初中数学 来源: 题型:
 老师布置了一道考题:如图所示,点M、N分别在正△ABC的边BC、CA上,且BM=CN,AM交BN于点Q.
老师布置了一道考题:如图所示,点M、N分别在正△ABC的边BC、CA上,且BM=CN,AM交BN于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:
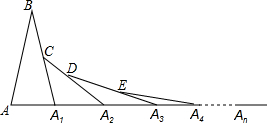 如图,在第1个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…按此作法进行下去,第n个三角形的以An为顶点的内角的度数为
如图,在第1个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…按此作法进行下去,第n个三角形的以An为顶点的内角的度数为查看答案和解析>>
科目:初中数学 来源: 题型:
| 月份 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 |
| 钱数变化 | 300 | 220 | -150 | -100 | 340 | 200 | 280 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com