练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
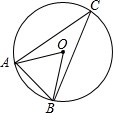
    1．已知：如图，AO、BO是⊙O的两条半径，点C在⊙O上，∠ACB=30°，则∠ABO的度数为（　　）
    A．30°B．45°C．50°D．60°

    分析 根据圆周角定理求出∠AOB，根据等腰三角形性质得出∠OBA=∠OAB，根据三角形内角和定理求出即可．

    解答 解：∵∠ACB=30°，
    ∴∠AOB=2∠ACB=60°，
    ∵OA=OB，
    ∴∠ABO=∠BAO=$\frac{1}{2}$×（180°-∠AOB）=60°，
    故选D．

    点评 本题考查了圆周角定理，等腰三角形性质，三角形的内角和定理的应用，解此题的关键是求出∠AOB度数和得出∠OAB=∠OBA．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

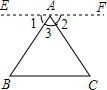    11．已知△ABC，求证∠A+∠B+∠C=180°．请在括号里填上适当的理由．
    证明：过点A作直线EF∥BC
    ∴∠1=∠B，∠2=∠C两直线平行，内错角相等
    ∵EF是一条直线
    ∴∠EAF=180°平角的定义
    又∵∠EAF=∠1+∠2+∠3
    ∴∠1+∠2+∠3=180°平角的定义
    ∴∠3+∠B+∠C=180°等量代换．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

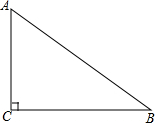    12．如图，在Rt△ABC中，∠C=90°，sinB=$\frac{3}{5}$，BC=5cm，以点C为圆心，以3cm的长为半径作圆，则⊙C与AB的位置关系是（　　）
    A．相离B．相交C．相切D．相切或相交

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知△ABC中，∠A=2∠B，∠A=90°，求证：a2-b2=bc．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．为加强学生身体锻炼，我校开展体育“大课间”活动．学校学生会体育部决定在学生中开设A：篮球，B：立定跳远，C：跳绳，D：跑步，E：排球五种活动项目．为了了解学生对五种项目的喜欢情况，随机抽取了部分学生进行调查，并将调查结果绘制成如下图所示的两个统计图．请结合图中的信息解答下列问题：
    （1）在这项调查中，共调查了多少名学生？
    （2）请计算本项调查中喜欢“篮球”的学生人数和所占百分比，并将两个统计图补充完整；
    （3）若该校有1200名在校学生，请估计喜欢排球的学生大约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知：如图，在平行四边形ABCD中，E、F分别是边AB和DC上的点，且BE=DF．求证：AF=CE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

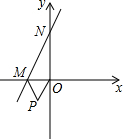    13．如图，已知直线y=2x+6与x轴、y轴分别交于M，N两点，以OM为边在x轴下方作等边三角形OMP，现将△OMP沿y轴向上平移，当点P恰好落在直线MN上时，点P运动的路程为$\frac{3}{2}$$\sqrt{3}$+3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

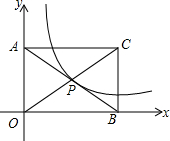    10．如图，矩形AOBC的面积为8，反比例函数y=$\frac{k}{x}$的图象经过矩形对角线的交点P，则反比例函数的解析式为y=$\frac{2}{x}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

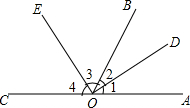    11．∠AOB与∠BOC互为补角，OD平分∠AOB，∠3+∠2=90°，如图所示．求证∠BOE=$\frac{1}{2}$∠BOC．请完成下列证明．
    证明：因为∠AOB与∠BOC互为补角（已知），
    所以∠AOB+∠BOC=180°（补角的定义），
    即L1+∠2+∠3+∠4=180°，又∵∠2+∠3=90°（已知），
    ∴∠1+∠4=90°（等式的性质），
    即∠1与L4互余，∠2与∠3互余（角平分线的定义　）
    因为OD平分∠AOB，所以∠1=∠2（角平分线的定义　），
    所以∠3=∠4（余角的性质　）
    即∠BOE=$\frac{1}{2}$∠BOC．

    查看答案和解析>>

    同步练习册答案