
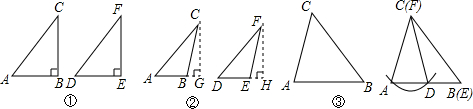
分析 (1)根据直角三角形全等的方法“HL”证明;
(2)过点C作CG⊥AB交AB的延长线于G,过点F作FH⊥DE交DE的延长线于H,根据等角的补角相等求出∠CBG=∠FEH,再利用“角角边”证明△CBG和△FEH全等,根据全等三角形对应边相等可得CG=FH,再利用“HL”证明Rt△ACG和Rt△DFH全等,根据全等三角形对应角相等可得∠A=∠D,然后利用“角角边”证明△ABC和△DEF全等;
(3)以点C为圆心,以AC长为半径画弧,与AB相交于点D,E与B重合,F与C重合,得到△DEF与△ABC不全等;
(4)根据三种情况可得结论,∠B不小于∠A即可.
解答 解:(1)△ABC与△DEF一定全等,依据的判定方法是HL;
(2)证明:如图,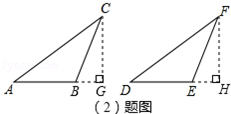
过点C作CG⊥AB交AB的延长线于G,过点F作DH⊥DE交DE的延长线于H,
∵∠B=∠E,且∠B、∠E都是钝角,
∴180°-∠B=180°-∠E,
即∠CBG=∠FEH,
在△CBG和△FEH中,
$\left\{\begin{array}{l}{∠CBG=∠FEH}\\{∠G=∠H}\\{BC=EF}\end{array}\right.$,
∴△CBG≌△FEH(AAS),
∴CG=FH,
在Rt△ACG和Rt△DFH中,
$\left\{\begin{array}{l}{AC=DF}\\{CG=FH}\end{array}\right.$,
∴Rt△ACG≌Rt△DFH(HL),
∴∠A=∠D,
在△ABC和△DEF中,
$\left\{\begin{array}{l}{∠A=∠D}\\{∠B=∠E}\\{AC=DF}\end{array}\right.$,
∴△ABC≌△DEF(AAS);
(3)小明的结论是:有两边和其中一边的对角对应相等的两个三角形不一定全等;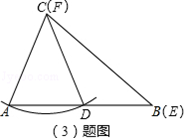
(4)若∠B≥∠A,则△ABC≌△DEF.
如图,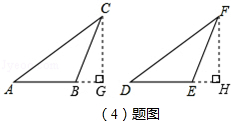
过点C作CG⊥AB交AB的延长线于G,过点F作DH⊥DE交DE的延长线于H,
∵∠B=∠E,且∠B、∠E都是锐角,
∴180°-∠B=180°-∠E,
即∠CBG=∠FEH,
在△CBG和△FEH中,
$\left\{\begin{array}{l}{∠CBG=∠FEH}\\{∠G=∠H}\\{BC=EF}\end{array}\right.$,
∴△CBG≌△FEH(AAS),
∴CG=FH,
在Rt△ACG和Rt△DFH中,
$\left\{\begin{array}{l}{AC=DF}\\{CG=FH}\end{array}\right.$,
∴Rt△ACG≌Rt△DFH(HL),
∴∠A=∠D,
在△ABC和△DEF中,
$\left\{\begin{array}{l}{∠A=∠D}\\{∠B=∠E}\\{AC=DF}\end{array}\right.$,
∴△ABC≌△DEF(AAS).
点评 本题考查了全等三角形的性质和判定的应用,能求出Rt△ABD≌Rt△ACD是解此题的关键,注意:全等三角形的对应角相等,对应边相等


科目:初中数学 来源: 题型:选择题
| A. | x1=1,x2=-5 | B. | x1=-1,x2=-5 | C. | x1=1,x2=5 | D. | x1=-1,x2=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品牌类型 | 月租费(元) | 必选业务套餐费(元) | 本地通话费(元/分钟) | 长途通话费(元/分钟) |
| 动感地带 | 0 | 18 | 0.3 | 0.6 |
| 神州行 | 10 | 5 | 0.4 | 0.6 |
| 全球通 | 0 | 68 | 1~288分钟免费,超过288分钟 0.2元/分钟(不区分长途通话和本地通话) | |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
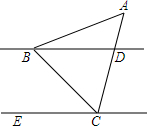 如图,在△ABC中,AB=AC,∠BAC=50°,点D在AC上,作直线BD,过C作CE∥BD,若∠BCE=40°,则∠ABD的度数是( )
如图,在△ABC中,AB=AC,∠BAC=50°,点D在AC上,作直线BD,过C作CE∥BD,若∠BCE=40°,则∠ABD的度数是( )| A. | 10° | B. | 15° | C. | 25° | D. | 65° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
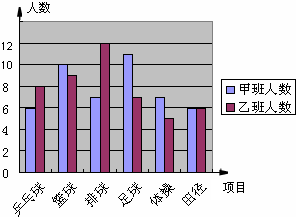
| A. | 甲班打乒乓球人数比乙班少2个 | B. | 甲班踢足球人数比乙班多3个 | ||
| C. | 这两班练体操的人数最少 | D. | 这两班练田径的人数不同 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com