
【题目】如图,抛物线y=﹣ ![]() x2+bx+c与y轴交于点C,与x轴交于A、B两点(点A在原点左侧,点B在原点右侧),且∠ACB=90°,tan∠BAC=
x2+bx+c与y轴交于点C,与x轴交于A、B两点(点A在原点左侧,点B在原点右侧),且∠ACB=90°,tan∠BAC= ![]() .
.
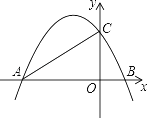
①求抛物线的解析式;
②若抛物线顶点为P,求四边形APCB的面积.
【答案】①y=﹣ ![]() x2﹣
x2﹣ ![]() x+ 2;②
x+ 2;②![]() .
.
【解析】
①由y=-![]() x2+bx+c=c,可求得C(0,c),由tan∠BAC=
x2+bx+c=c,可求得C(0,c),由tan∠BAC=![]() ,可设A(-2c,0),B(
,可设A(-2c,0),B(![]() c,0),把A(-2c,0),B(
c,0),把A(-2c,0),B(![]() c,0)代入y=-
c,0)代入y=-![]() x2+bx+c=c求得b,c,即可求得求抛物线的解析式;
x2+bx+c=c求得b,c,即可求得求抛物线的解析式;
②解方程-![]() x2-
x2-![]() x+
x+![]() =0可求得A,B点的坐标,由于四边形APCB的面积=S△AOP+S△POC+S△COB,根据三角形的面积公式即可求得结论.
=0可求得A,B点的坐标,由于四边形APCB的面积=S△AOP+S△POC+S△COB,根据三角形的面积公式即可求得结论.
①令x=0则y=﹣![]() x2+bx+c=c,
x2+bx+c=c,
∴C(0,c),
∵tan∠BAC=![]() ,
,
∴A(﹣2c,0),
∠ACB=90°,
∴∠BCO=∠BAC,
∴OB=![]() OC=
OC=![]() c,
c,
∴B(![]() c,0),
c,0),
把A(﹣2c,0),B( ![]() c,0)代入y=﹣
c,0)代入y=﹣![]() x2+bx+c=c,
x2+bx+c=c,
得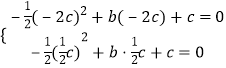 ,
,
解得: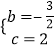 ,
,
求抛物线的解析式为y=﹣![]() x2﹣
x2﹣![]() x+ 2;
x+ 2;
②y=﹣![]() x2﹣
x2﹣![]() x+2=﹣
x+2=﹣![]() (x+
(x+![]() )2+
)2+![]() ,
,
∴P(﹣![]() ,
,![]() ),
),
令﹣![]() x2﹣
x2﹣![]() x+2=0,解得:x1=﹣1,x2=
x+2=0,解得:x1=﹣1,x2=![]() ,
,
∴A(﹣4,0),B( 1,0)
连接AP,PC,CB,PO,则四边形APCB的面积=S△AOP+S△POC+S△COB=![]() ×4×
×4×![]() +
+![]() ×2×
×2×![]() +
+![]() ×1×2=
×1×2=![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,点A在抛物线y=x2﹣2x+2上运动,过点A作AC上x轴于点C,以AC为对角线作矩形ABCD,连结BD,则BD的最小值为( )
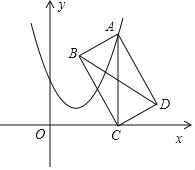
A. ![]() B. 1 C.
B. 1 C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,两个小圆的半径分别是2厘米和3厘米,最外侧大圆的面积是半径为2厘米的小圆面积的几倍?阴影部分的面积是半径为3厘米的圆的面积的多少?
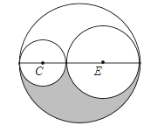
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为4cm,则Rt△MBN的周长为________cm.
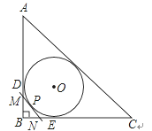
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿![]() 的方向运动,到达点C时停止,设运动时间为x(秒),
的方向运动,到达点C时停止,设运动时间为x(秒),![]() ,则y关于x的函数的图像大致为( )
,则y关于x的函数的图像大致为( )
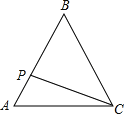
A. 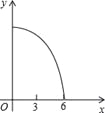 B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k为常数,k≠1).
(k为常数,k≠1).
(Ⅰ)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(Ⅱ)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(Ⅲ)若其图象的一支位于第二象限,在这一支上任取两点A(x1,y1)、B(x2,y2),当y1>y2时,试比较x1与x2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
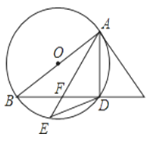
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.
(1)求证:FD=DC;
(2)若AE=8,DE=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的![]() ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com