【题目】小明有5张写着不同数字的卡片，请按要求抽出卡片，完成下列各问题：
（1）从中取出2张卡片，使这2张卡片上数字的乘积最大，如何抽取？最大值是多少？答：我抽取的2张卡片是________、________，乘积的最大值为________．
（2）从中取出2张卡片，使这2张卡片上数字相除的商最小，如何抽取？最小值是多少？答：我抽取的2张卡片是________、________，商的最小值为________．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】已知矩形ABCD，AB＝6，AD＝8，将矩形ABCD绕点A顺时针旋转θ（0°＜θ＜360°）得到矩形AEFG，当θ＝_____°时，GC＝GB．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】【问题学习】小芸在小组学习时问小娟这样一个问题：已知α为锐角，且sin α＝
，求sin 2α的值．
小娟是这样给小芸讲解的：
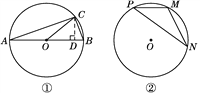
如图①，在⊙O中，AB是直径，点C在⊙O上，所以∠ACB＝90°. 设∠BAC＝α，则sin α＝
＝.易得∠BOC＝2α.设BC＝x，则AB＝3x，AC＝2
x.作CD⊥AB于D，求出CD＝________(用含x的式子表示)，可求得sin 2α＝
＝________.
【问题解决】已知，如图②，点M，N，P为⊙O上的三点，且∠P＝β，sin β＝
，求sin 2β的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解：
为解方程（x2﹣1）2﹣5（x2﹣1）+4=0，我们可以将x2﹣1视为一个整体，然后设x2﹣1=y，则原方程化为y2﹣5y+4=0，解此方程得：y1=1，y2=4．
当y=1时，x2﹣1═1，∴x=±
．
当y=4时，x2﹣1═4，∴x=±
．
∴原方程的解为：x1=，x2=﹣，x3=，x4=﹣．
以上方法叫做换元法解方程，达到了降次的目的，体现了转化思想．
运用上述方法解方程：x4﹣8x2+12=0．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，延长AB到点C，使得2BC=3OB，D是⊙O上一点，连接AD，CD，过点A作CD的垂线，交CD的延长线于点F，过点D作DE⊥AC于点E，且DE=DF．
（1）求证：CD是⊙O的切线；
（2）若AB=4．
①求DF的长；
②连接OF，交AD于点M，求DM的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在数轴上，A1、P两点表示的数分别为1、3，A1、A2关于O对称，A2、A3关于点P对称，A3、A4关于点O对称，A4、A5关于点P对称…依次规律，则点A15表示的数是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
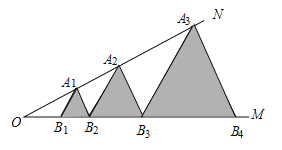
【题目】如图已知:
点
···，在射线
上，点
，···，在射线
上，
，···，均为等边三角形，若
则
的边长为________________________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将函数y=
（x﹣2）2+1的图象沿y轴向上平移得到一条新函数的图象，其中点A（1，m），B（4，n）平移后的对应点分别为点A'、B'．若曲线段AB扫过的面积为9（图中的阴影部分），则新图象的函数表达式是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
