
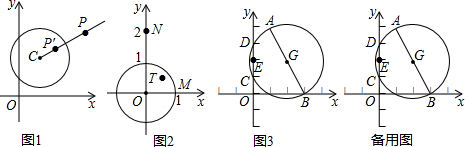
���� ��1�����÷��ݵ㶨�壬�������ON�䣬OT�䣬OM��ij��ȣ�Ȼ��������ǵ����ꣻ
��2���������E��G��O��G��O��E�䣬���ù��ɶ����涨��֤����E��O��G��RT����
�ڿ����������Σ���P��ֱ��AB���Ҷ����ڣ�
��� �⣺��1����ON•ON��=1��ON=2��
��ON��=$\frac{1}{2}$���෴�ݵ�N�����꣨0��$\frac{1}{2}$����
��OM•OM��=1��OM=1��
��OM��=1
���ݵ�M�����꣨1��0��
��$OT•OT��=1��OT=\frac{\sqrt{2}}{2}$��
��$OT��=\sqrt{2}$��
��T���ڵ�һ���Ľ�ƽ�����ϣ�
�෴�ݵ�T�����꣨1��1��
��2���������⣺AB=2$\sqrt{5}$��r=$\sqrt{5}$��
��E��0��2����G��2��2����EG=2��E��G•EG=5��
��$E��G=\frac{5}{2}$��
��OG•O��G=5��OG=2$\sqrt{5}$��
��O��G=$\frac{\sqrt{5}}{2}$��
��E�䣨-$\frac{1}{2}$��2����O�䣨$\frac{3\sqrt{5}}{2}$��$\frac{3\sqrt{5}}{2}$����
��O��E��=$\frac{\sqrt{5}}{2}$��
��E��G2=E��O��2+O��G2��
���E��O��G=90��
����ͼ���ߡ�BAP1=��OBC����CAP1+��CBP1=��CAB+��BAP1+��CBP1=180�㣬��OBC+��CBP1+��P1BQ1=180�㣬��CAB=45�㣬
���P1BQ1=45�㣬
�ߡ�AP1B=��BP1Q1=90�㣬
���PBQ1�ǵ���ֱ�������Σ�
�ɡ�AP1B�ס�BOC�õ���$\frac{AP1}{BP1}=\frac{BO}{CO}=3$��
��$AB=2\sqrt{5}$��
��$BP1=\sqrt{2}$��BQ1=2��Q1��5��0����
��Q1��G•GQ1=5��
��Q1��G=$\frac{5\sqrt{13}}{13}$��
�ߡ�P2AB=��BAP1��
��P1��P2����ֱ��AB�Գƣ���P1��4��1������֪��P2��$\frac{8}{5}$��-$\frac{1}{5}$����
��ֱ��AP2��Y=-7X+11����Q2��$\frac{11}{7}��0$����
�ɣ�Q2��G•Q2G=5�õ���Q2��G=$\frac{7\sqrt{205}}{41}$��
���� ����Ŀ�����֪ʶ��Ƚ϶࣬�õ�Բ�����ʣ�һ�κ��������ʣ����ɶ����涨���ȣ���Ŀ�ۺ��ԱȽ�ǿ�����õ����������α��磺��BP1Q1�ǵ���ֱ�������Σ����öԳ����������֪ʶ�㣮


 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ھ���ABCD�У�O�ǶԽ��ߵĽ��㣬OE��BC��E��0E=2����ACB=30�㣮�����ABCD�������
��ͼ���ھ���ABCD�У�O�ǶԽ��ߵĽ��㣬OE��BC��E��0E=2����ACB=30�㣮�����ABCD��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��C���߶�AB�ϣ���AB��ͬ�����ȱ������Ρ�ACM�͡�BCN������AN��BM��
��ͼ����֪��C���߶�AB�ϣ���AB��ͬ�����ȱ������Ρ�ACM�͡�BCN������AN��BM���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�AB=AC=8��BC=6����DΪBC��һ�㣬BD=2������D������DE��AC�ڵ�E��ʹ��ADE=��B��
��ͼ���ڡ�ABC�У�AB=AC=8��BC=6����DΪBC��һ�㣬BD=2������D������DE��AC�ڵ�E��ʹ��ADE=��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��PA��PB�ǡ�O�����ߣ�A��BΪ�е㣬��OAB=30�㣬OA=3������Ӱ�������Ϊ9$\sqrt{3}$-3�У�
��ͼ��PA��PB�ǡ�O�����ߣ�A��BΪ�е㣬��OAB=30�㣬OA=3������Ӱ�������Ϊ9$\sqrt{3}$-3�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com