
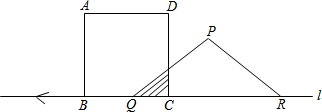
分析 (1)在等腰三角形PQR中,由PQ=PR=5cm,QR=8cm,根据相似三角形的性质表示出三角形的面积即可求出;
(2)利用相似三角形的性质得出各边长,进而根据三角形的面积公式即可求解.
解答 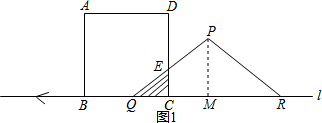 解:过点P作PM⊥QR于点M,
解:过点P作PM⊥QR于点M,
∵PQ=PR=5cm,QR=8cm,
∴QM=MR=4cm,则PM=3cm,
(1)如图1,当正方形ABCD与等腰三角形PQR重合部分的面积为5时,
即S△ECQ=5cm2,
由题意知,△QEC∽△QPM,
则$\frac{EC}{PM}$=$\frac{QC}{QM}$,
即$\frac{EC}{3}$=$\frac{t}{4}$,
故EC=$\frac{3}{4}$t,
∴$\frac{1}{2}$t•$\frac{3}{4}$t=5,
解得:t=$\frac{2\sqrt{30}}{3}$(负数舍去),
故$\frac{2\sqrt{30}}{3}$秒后正方形ABCD与等腰三角形PQR重合部分的面积为5.
同理可得:当RB=$\frac{2\sqrt{30}}{3}$cm时正方形ABCD与等腰三角形PQR重合部分的面积为5
故(5-$\frac{2\sqrt{30}}{3}$)秒后正方形ABCD与等腰三角形PQR重合部分的面积为5,
综上所述:t=$\frac{2\sqrt{30}}{3}$s或(5-$\frac{2\sqrt{30}}{3}$)秒时正方形ABCD与等腰三角形PQR重合部分的面积为5;
(2)由题意可得:S△PQM=$\frac{1}{2}$×4×3=6(cm2),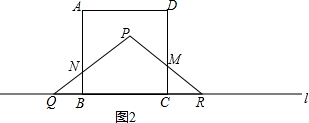
故当正方形ABCD与等腰三角形PQR重合部分的面积为7时,
则如图2所示:QC=t,则RC=8-t,QB=t-5,
故由(1)得:NB=$\frac{3}{4}$(t-5),MC=$\frac{3}{4}$(8-t)
可得S五边形NBCMP=S△PQR-S△NQB-S△MCR
=12-$\frac{1}{2}$×(8-t)×$\frac{3}{4}$(8-t)-$\frac{1}{2}$(t-5)×$\frac{3}{4}$(t-5)=7,
解得:t1=$\frac{39+\sqrt{159}}{6}$,t2=$\frac{39-\sqrt{159}}{6}$,
故$\frac{39+\sqrt{159}}{6}$秒或$\frac{39-\sqrt{159}}{6}$秒后正方形ABCD与等腰三角形PQR重合部分的面积为7.
点评 此题考查了一元二次方程的应用、正方形的性质、等腰三角形的性质、图形面积的求法等知识,利用相似三角形的性质得出各边长是解答此题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
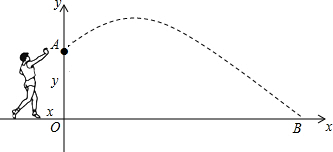 校运会上,小明参加铅球比赛,若某次试掷,铅球飞行的高度y(m)与水平距离x(m)之间的函数关系式为y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$,求:
校运会上,小明参加铅球比赛,若某次试掷,铅球飞行的高度y(m)与水平距离x(m)之间的函数关系式为y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$,求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (2,-1) | C. | (-1,2) | D. | (-1,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
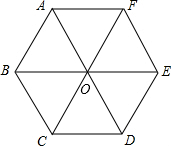 如图,正六边形ABCDEF是由边长为2厘米的六个等边三角形拼成,那么图中
如图,正六边形ABCDEF是由边长为2厘米的六个等边三角形拼成,那么图中查看答案和解析>>
科目:初中数学 来源: 题型:填空题
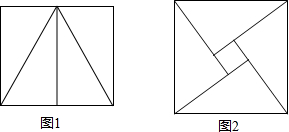 小华和小明分别用4个全等的直角三角形拼图:小华拼成的矩形(图1)的周长为20cm,小明拼成的正方形(图2)中有一边长为1cm的正方形小孔,则小明拼成的正方形的周长
小华和小明分别用4个全等的直角三角形拼图:小华拼成的矩形(图1)的周长为20cm,小明拼成的正方形(图2)中有一边长为1cm的正方形小孔,则小明拼成的正方形的周长查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com