Question

14．已知AB是⊙O内接正四边形的一边，AC是⊙O内接正六边形的一边，则∠BAC的度数为（　　）

• A． 105°
• B． 150°
• C． 30°
• D． 105°或15°

Answer 1

分析 根据题意画出图形，根据正方形与正六边形的性质求出$\widehat{AB}=\widehat{AC}$的度数，根据圆周角与弦的关系即可得出结论．

解答 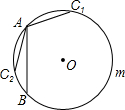解：如图所示，
∵AB是⊙O内接正方形的一条边长，AC是同一个⊙O内接正六边形的一条边长，
∴$\widehat{AB}$的度数=$\frac{360°}{4}$=90°，$\widehat{AC}$的度数=$\frac{360°}{6}$=60°．
当点C在C₁的位置时，
∵优弧$\widehat{BmC}$的度数=360°-90°-60°=210°，
∴∠BAC₁=$\frac{1}{2}$×210°=105°；
当点C在C₂的位置时，$\widehat{B{C}_{2}}$的度数=90°-60°=30°，
∴∠BAC₂=$\frac{1}{2}$×30°=15°．
综上所述，∠BAC的度数是105°或15°．
故选D．

点评 本题考查的是正多边形和圆，在解答此题时要进行分类讨论，不要漏解．