
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
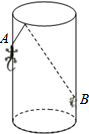 如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,求壁虎捕捉蚊子的最短距离.(容器厚度忽略不计)
如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,求壁虎捕捉蚊子的最短距离.(容器厚度忽略不计)查看答案和解析>>
科目:初中数学 来源: 题型:
| A、1 | B、3 | C、7 | D、5 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| A、三角形可分为斜三角形、直角三角形和锐角三角形 |
| B、等腰三角形任何一个内角都有可能是钝角或直角 |
| C、三角形外角一定是钝角 |
| D、在△ABC中,如果∠A=∠B=∠C,那么∠A=60°,∠C=60° |
查看答案和解析>>
科目:初中数学 来源: 题型:
| pq+1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| pq+1 |
| q |
| 1 |
| n2 |
| 5 |
| n |
| 1 |
| m |
| 1 |
| n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com