
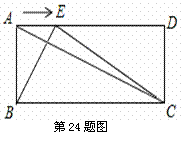
如图,已知在矩形ABCD中,AB = a,BC = b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.
(1)若a = 5,sin∠ACB =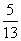 ,求的长。(3分)
,求的长。(3分)
(2)若a = 5,b=10当BE⊥AC时,求出此时AE的长.(4分)
 (3)设
(3)设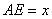 ,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.(5分)
,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.(5分)
解:(1)① b = 12 ……………………………3分
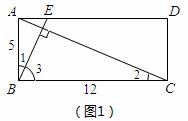
(2)如图1,∵BE⊥AC
∴∠2 + ∠3 = 900
 又∠1 + ∠3 = 900
又∠1 + ∠3 = 900
∴∠1 = ∠2
又∠BAE = ∠ABC = 900
∴△AEB ∽△BAC ………………………5分
∴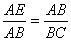 即
即 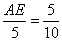
∴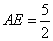 ………………………………7分
………………………………7分
(3)∵点E在线段AD上的任一点,且不与A、D重合,
∴当△ABE与△BCE相似时,则∠BEC = 900
所以当△BAE ∽△CEB(如图2)
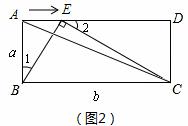 则∠1 = ∠BCE,
则∠1 = ∠BCE,
又BC∥AD
∴∠2 = ∠BCE
∴∠1 = ∠2
又∠BAE = ∠EDC = 900
∴△BAE ∽△EDC
∴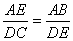 即
即 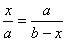
∴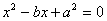 …………………………………9分
…………………………………9分
即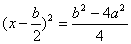
当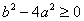
∵a>0,b>0, ∴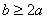
即 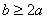 时,
时,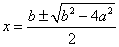 ……………………11分
……………………11分
综上所述:当a、b满足条件b = 2a时△BAE ∽△CEB,此时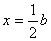 (或x = a);
(或x = a);
当a、b满足条件b>2a时△BAE ∽△CEB,此时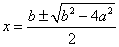


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
为弘扬校园文化建设,某校开展了题为“做最美中学生”演讲比赛,在安排1位女选手和3位男选手的出场顺序时,采用随机抽签方式.
(1)请直接写出第一位出场是女选手的概率;
(2)请你用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果,并求出他们都是男选手的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC 中,∠C=90°,D 是 AC 上一点,DE⊥AB 于点 E,若 AC=8,BC=6,DE=3,则 AD 的长为( )
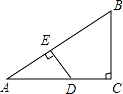
A.3 B.4 C.5 D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com