
 如图,△BCD的各个顶点都在⊙A上,△BCD的角平分线BF交CD于点E,交⊙A于点F,连结CF,求证:BE2=BC•BD-EC•ED.
如图,△BCD的各个顶点都在⊙A上,△BCD的角平分线BF交CD于点E,交⊙A于点F,连结CF,求证:BE2=BC•BD-EC•ED.| BC |
| BE |
| BF |
| BD |
 解:如图,∵BF平分∠CBD,
解:如图,∵BF平分∠CBD,| BC |
| BE |
| BF |
| BD |


科目:初中数学 来源: 题型:
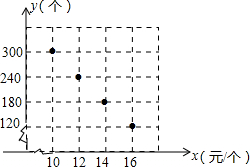 某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.这种许愿瓶的进价为6元/个,根据市场调查,一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:
某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.这种许愿瓶的进价为6元/个,根据市场调查,一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:
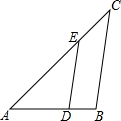 如图所示,已知DE∥BC,AE=50cm,EC=30cm,BC=70cm,∠A=45°,∠C=40°,求:
如图所示,已知DE∥BC,AE=50cm,EC=30cm,BC=70cm,∠A=45°,∠C=40°,求:查看答案和解析>>
科目:初中数学 来源: 题型:
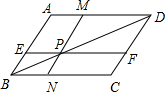 如图,?ABCD中,EF∥AD,MN∥AB,MN与EF交于点P,且点P在BD上.
如图,?ABCD中,EF∥AD,MN∥AB,MN与EF交于点P,且点P在BD上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com