
| A. | x1=-2,x2=-$\frac{3}{2}$ | B. | x1=2,x2=$\frac{3}{2}$ | ||
| C. | x1=-$\frac{6}{7}$ | D. | x1=-2,x2=-$\frac{3}{2}$,x3=-$\frac{6}{7}$ |
分析 解不等式组根据m为整数求得m=1或m=2,代入方程分别求解即可得.
解答 解:解不等式2m-1>0得:m>$\frac{1}{2}$,
解不等式4-2m>-1得:m<$\frac{5}{2}$,
∴$\frac{1}{2}$<m<$\frac{5}{2}$,
又∵m为整数,
∴m=1或m=2,
方程整理可得(m2-m-2)x2-7x-6=0,
当m=1时,方程为2x2+7x+6=0,
∵(x+2)(2x+3)=0,
∴x=-2或x=-$\frac{3}{2}$
当m=2时,方程为-7x-6=0,
解得:x=-$\frac{6}{7}$,
故选:D.
点评 本题主要考查解一元一次不等式组和一元二次方程的能力,熟练掌握解不等式组和一元二次方程的基本技能是解题的关键.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
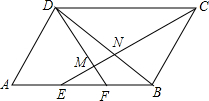 如图,?ABCD中,AE=EF=FB,CE交DF,DB于M,N,则EM:MN:NC=( )
如图,?ABCD中,AE=EF=FB,CE交DF,DB于M,N,则EM:MN:NC=( )| A. | 5:4:12 | B. | 5:3:12 | C. | 4:3:5 | D. | 2:1:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
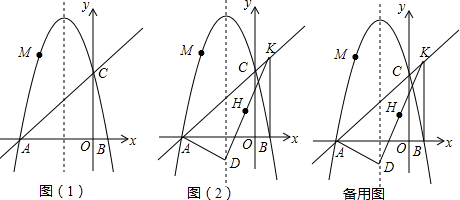
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com