
����Ŀ����ͼ1��ͼ3�У���B���߶�AC���е㣬��D���߶�CE���е㣮�ı���BCGF���ı���CDHN���������Σ�AE���е���M��
(1)��ͼ1����E��AC���ӳ����ϣ���N���G�غ�ʱ����M���C�غϣ���֤��FM=MH��FM��MH��
(2)��ͼ1�е�CE�Ƶ�C˳ʱ����תһ����ǣ��õ�ͼ2����֤����FMH�ǵ���ֱ�������Σ�
(3)��ͼ2�е�CE���̵�ͼ3���������FMH���ǵ���ֱ����������(����˵������)

���𰸡�(1)֤����������(2)֤����������(3)��FMH���ǵ���ֱ�������Σ�
��������
(1)���������ε����ʿɵ�FB=BM=MD=DH��Ȼ���������߽DZ���֤����FBM����MDHȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�FM=MH���������FMH=90�����õ�FM��HM��Ȼ����ݵ���ֱ�������εĶ���֤�����ɣ�(2)����MB��MD����FM��AC���ڵ�P�����������ε���λ��ƽ���ڵ����߲��ҵ��ڵ����ߵ�һ��ɵ�MD��BC����MD=BC=BF��MB��CD����MB=CD=DH��Ȼ��õ��ı���BCDM��ƽ���ı��β������CBM=��CDM���������FBM=��MDH��Ȼ���������߽DZ���֤����FBM����MDHȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�FM=MH��ȫ�������ζ�Ӧ����ȿɵá�MFB=��HMD��������ֱ��ƽ�У��ڴ�����ȿɵá�APM=��FMD��Ȼ����������ε�һ����ǵ������������ڵ������ڽǵĺ������FMH=��FBP=90�����ٸ��ݵ���ֱ�������εĶ���֤�����ɣ�(3)֤������ͬ(2)��
(1)֤�������ı���BCGFΪ�����Σ�
��BF=BM=MN����FBM=90����
���ı���CDHNΪ�����Σ�
��DM=DH=MN����HDM=90����
��BF=BM=MN��DM=DH=MN��
��BF=BM=DM=DH��
��BF=DH����FBM=��HDM��BM=DM��
���FBM�ա�HDM��
��FM=MH��
�ߡ�FMB=��DMH= 45����
���FMH=90����
��FM��HM��
(2)֤��������MB��MD����ͼ2����FM��AC���ڵ�P��
��B��D��M�ֱ���AC��CE��AE���е㣬
��MD��BC����MD=![]() AC=BC=BF��MB��CD����MB=
AC=BC=BF��MB��CD����MB=![]() CE=CD=DH��
CE=CD=DH��
���ı���BCDM��ƽ���ı��Σ�
���CBM=��CDM��
�ߡ�FBP=��HDC��
���FBM=��MDH��
��MD =BF����FBM=��MDH��MB=DH��
���FBM�ա�MDH��SAS����
��FM=MH���ҡ�MFB=��HMD��
��BC��MD��
���APM=��FMD��
���FMH=��FMD-��HMD=��APM-��MFB=��FBP=90����
���FMH�ǵ���ֱ�������Σ�

(3)��FMH���ǵ���ֱ�������Σ�
����MB��MD����ͼ3����FM��AC���ڵ�P��
��B��D��M�ֱ���AC��CE��AE���е㣬
��MD��BC����MD=BC=BF��MB��CD����MB=CD=DH��
���ı���BCDM��ƽ���ı��Σ�
���CBM=��CDM��
�֡ߡ�FBP=��HDC��
���FBM=��MDH��
����FBM����MDH��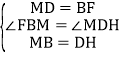 ��
��
���FBM�ա�MDH��SAS����
��FM=MH���ҡ�MFB=��HMD��
��BC��MD��
���APM=��FMD��
���FMH=��FMD-��HMD=��APM-��MFB=��FBP=90����
���FMH�ǵ���ֱ�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ� �Ͽ�ʱ����ʦ�������һ�����⣺��������ʵ��x������x�IJ���ʽx2��2x��1��a��0���������a��ȡֵ��Χ��
С�ݵ�˼·�ǣ�ԭ����ʽ�ȼ���x2��2x��1��a���躯��y1=x2��2x��1��y2=a����������������ͼ���ʾ��ͼ������ԭ����ת��Ϊ����y1��ͼ����y2��ͼ���Ϸ�ʱa��ȡֵ��Χ��
����С�ݵ�˼·�ش�
��������ʵ��x������x�IJ���ʽx2��2x��1��a��0���������a��ȡֵ��Χ�ǣ�
�ο�С��˼������ķ�����������⣺
����x�ķ���x��4= ![]() ��0��a��4��Χ���������⣬��a��ȡֵ��Χ��
��0��a��4��Χ���������⣬��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2017��8��1�����й������ž�����90��������գ�ijѧУ��ίΪ�������С�ѧ����衱��ӽ������Ҫȷ��һ��ϲ���������ĸ���Ϊÿ��س���Ŀ��Ϊ���ṩ����ΪA��B��C��D���ױ�ѡ��Ŀ��ѧ��ѡ�����������飬�����ɼ������ݻ�������������������ͳ��ͼ�������ͼ�١�ͼ�����ṩ����Ϣ������������⣺ 
��1�����γ��������ѧ������������ѡ����Ŀ����ΪA��ѧ������ӦԲ�ĽǵĶ���Ϊ��
��2���뽫ͼ�ڲ���������
��3������У����1800��ѧ�������ݳ�������Ľ������ȫУ���ж�����ѧ��ѡ�����ΪC����ĿΪ�س�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABCΪ���������Σ�AB��AC����DΪֱ��BC��һ���㣨��D�����B����C�غϣ�����ADΪ������ADE����AD��AE������CE����BAC����DAE��
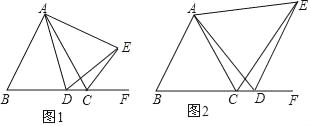
��1����ͼ1������D�ڱ�BC��ʱ����˵�����١�ABD�ա�ACE����BC��DC+CE��
��2����ͼ2������D�ڱ�BC���ӳ�����ʱ�������������䣬̽���߶�BC��DC��CE֮����ڵ�������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
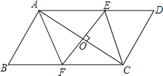
����Ŀ����ͼ����ABCD�У�ACΪ�Խ��ߣ�EF��AC�ڵ�O,��AD�ڵ�E,��BC�ڵ�F������AF��CE.����̽����O������ʲô����ʱ���ı���AFCE�����Σ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ij��ѧ��ѧ�С����ѧϰ�ˡ��������Ǻ�����ߡ���ѡ������С�Ӷ�һ��������BC�ĸ߶ȣ���������б���ϵ�D������ý����ﶥ������Ϊ30�㣮��D�����ĸ߶�DE=5m���µ�EA=10m��Ȼ����A����ý����ﶥB��������50�㣬��E��A��C��ͬһˮƽ���ϣ�������BC�ĸߣ����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���˵Ĵ������ܼ�������������ģ�����ʱ������ƣ�����Ķ���������������������ѧ������ʦ�������Լ���ѧ����ѧϰ�������ɣ������ݵ������������һ�����ߣ���ͼ��ʾ�������������ʾѧϰ�еļ��䱣�����������ʾʱ�䣬�۲�ͼ�ش��������⣺

��1���۲�ͼ��![]() ���䱣����ԼΪ ��
���䱣����ԼΪ ��![]() ���䱣����ԼΪ ��
���䱣����ԼΪ ��
��2��ͼ�е�![]() ���ʾ��������ʲô��
���ʾ��������ʲô��
![]() ���ʾ�������� ��
���ʾ�������� ��
�������ĸ�ʱ������������ٶ���죿����� ��
��0��2![]() ����2��4
����2��4![]() �� ��4��6
�� ��4��6![]() �� ��6��8
�� ��6��8![]()
��3������ʦÿ�ڿν���ʱ����Ա��ڿν����ܽ�عˣ���Ҫ��ѧ��ÿ��������˯ǰ�Ե�����������ǵĿ��ñʼǽ��и�ϰ���ݵ�������һ���������ܱ���98�������ѧ��һ�첻��ϰ������ֻ��������ɴˣ����ܸ����������߹����ƶ�������������ٵ�ѧϰ�ƻ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=����x��1��2+c��x�ύ��A��B��A��B�ֱ���y����������ࣩ���㣬��y��������ύ�ڵ�C������ΪD����֪A����1��0����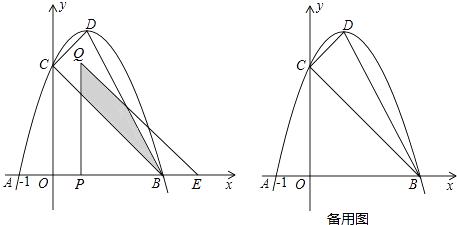
��1�����B��C�����ꣻ
��2���жϡ�CDB����״��˵�����ɣ�
��3������COB��x������ƽ��t����λ���ȣ�0��t��3���õ���QPE����QPE���CDB�ص����֣���ͼ����Ӱ���֣����ΪS����S��t�ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��y= ![]() x+1�ǹ���x��һ�κ�������һԪ���η���kx2+2x+1=0�ĸ������Ϊ�� ��
x+1�ǹ���x��һ�κ�������һԪ���η���kx2+2x+1=0�ĸ������Ϊ�� ��
A.û��ʵ����
B.��һ��ʵ����
C.����������ȵ�ʵ����
D.��������ȵ�ʵ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com