
 如图,正方形ABCD中,E为AB中点,EF⊥DE且BF平分∠CBM,求证:DE=EF.
如图,正方形ABCD中,E为AB中点,EF⊥DE且BF平分∠CBM,求证:DE=EF.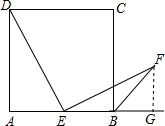 证明:作FG⊥AM于G,
证明:作FG⊥AM于G,| AE |
| AD |
| FG |
| EG |
| 1 |
| 2 |
|


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案科目:初中数学 来源: 题型:
 如图,已知半⊙O的直径AB=12,AD、BC、CD是⊙O的切线,E是半⊙O上的动切点,AD=x,BC=y.
如图,已知半⊙O的直径AB=12,AD、BC、CD是⊙O的切线,E是半⊙O上的动切点,AD=x,BC=y.查看答案和解析>>
科目:初中数学 来源: 题型:
 小明在画函数y=|x|的图象时,得到了如图甲所示的图象.他发现这个图象好像是把函数y=x的图象x轴下方的部分翻折到x轴上方(如图乙).于是他得出这样的结论:y=|kx+b|的图象都可以这样做,你认为他的结论正确吗?能由y=kx+b的图象得到y=|kx+b|的图象吗?
小明在画函数y=|x|的图象时,得到了如图甲所示的图象.他发现这个图象好像是把函数y=x的图象x轴下方的部分翻折到x轴上方(如图乙).于是他得出这样的结论:y=|kx+b|的图象都可以这样做,你认为他的结论正确吗?能由y=kx+b的图象得到y=|kx+b|的图象吗?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
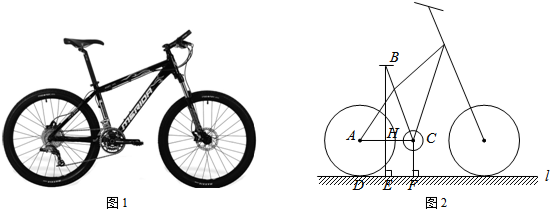
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com