【题目】阅读材料：①韦达定理:设一元二次方程ax2+bx+c=0（且a≠0）中，两根
有如下关系:
,
.
②已知p2﹣p﹣1=0，1﹣q﹣q2=0，且pq≠1，求
的值．
解：由p2﹣p﹣1=0及1﹣q﹣q2=0，可知p≠0，q≠0．
又∵pq≠1，∴
；
∴1﹣q﹣q2=0可变形为
的特征．
所以p与
是方程x2﹣x﹣1=0的两个不相等的实数根．
则p+=1，
∴=1.
根据阅读材料所提供的方法，完成下面的解答．
已知：2m2﹣5m﹣1=0，
，且m≠n．求：
的值．
长江作业本同步练习册系列答案科目：初中数学 来源： 题型：
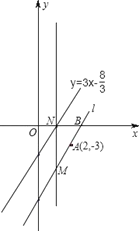
【题目】如图，在平面直角坐标系中，直线 l 经过点A(2，﹣3)，与 x 轴交于点 B，且与直线y=3x-
平行．
(1)求直线l的函数解析式及点B的坐标；
(2)如直线l上有一点 M(a，﹣6)，过点 M 作 x 轴的垂线，交直线 y=3x-于点N，在线段MN上求一点P，使△PAB是直角三角形，请求出点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，已知等边△ABC的两个顶点的坐标为A（－4，0），B（2，0）．
（1）用尺规作图作出点C，并求出点C的坐标；
（2）求△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
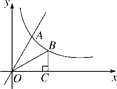
【题目】如图，直线y＝2x与反比例函数y＝
(k≠0，x＞0)的图象交于点A(1，a)，点B是此反比例函数图象上任意一点(不与点A重合)，BC⊥x轴于点C.
(1)求k的值；
(2)求△OBC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】平行四边形ABCD在平面直角坐标系中的位置如图所示，其中A（﹣4，0），B（2，0），C（3，3）反比例函数
的图象经过点C．
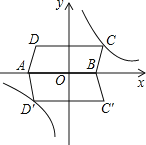
（1）求此反比例函数的解析式；
（2）将平行四边形ABCD沿x轴翻折得到平行四边形AD′C′B，请你通过计算说明点D′在双曲线上；
（3）请你画出△AD′C，并求出它的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在边长为1的正方形网格中，两个三角形的顶点都在格点（网线的交点）上，下列方案中不能把△ABC平移至△DEF位置的是（ ）
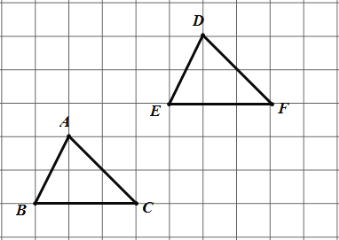
A.先把△ABC沿水平方向向右平移4个单位长度，再向上平移3个单位长度
B.先把△ABC向上平移3个单位长度，再沿水平方向向右平移4个单位长度
C.把△ABC沿BE方向移动5个单位长度
D.把△ABC沿BE方向移动6个单位长度
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道：x2﹣6x＝(x2﹣6x+9)﹣9＝(x﹣3)2﹣9；﹣x2+10＝﹣(x2﹣10x+25)+25＝﹣(x﹣5)2+25，这一种方法称为配方法，利用配方法请解以下各题：
(1)按上面材料提示的方法填空：a2﹣4a＝ ＝ ．﹣a2+12a＝ ＝ ．
(2)探究：当a取不同的实数时在得到的代数式a2﹣4a的值中是否存在最小值？请说明理由．
(3)应用：如图．已知线段AB＝6，M是AB上的一个动点，设AM＝x，以AM为一边作正方形AMND，再以MB、MN为一组邻边作长方形MBCN．问：当点M在AB上运动时，长方形MBCN的面积是否存在最大值？若存在，请求出这个最大值；否则请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，以□ABCD的顶点A为圆心，AB为半径作圆，分别交AD，BC于点E、F，延长BA交⊙A于G．
（1）求证：
.
（2）若
的度数为70°，求∠C的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
