
【题目】如图1,在矩形ABCD中,![]() ,
,![]() ,点E从点B出发,沿BC边运动到点C,连结DE,过点E作DE的垂线交AB于点F.
,点E从点B出发,沿BC边运动到点C,连结DE,过点E作DE的垂线交AB于点F.
![]() 求证:
求证:![]() ;
;
![]() 求BF的最大值;
求BF的最大值;
![]() 如图2,在点E的运动过程中,以EF为边,在EF上方作等边
如图2,在点E的运动过程中,以EF为边,在EF上方作等边![]() ,求边EG的中点H所经过的路径长.
,求边EG的中点H所经过的路径长.

【答案】(1)证明见解析;(2)当![]() 时,BF存在最大值
时,BF存在最大值![]() ;(3)点H所经过的路径长是
;(3)点H所经过的路径长是![]() .
.
【解析】分析:(1)依据∠BFE+∠BEF=90°,∠CED+∠BEF=90°,即可得到∠BFE=∠CED,再根据∠CED=∠ADE,即可得出∠BFE=∠ADE;
(2)依据△BEF∽△CDE,即可得到![]() ,设BE=x(0≤x≤3),则CE=3-x,根据BF=
,设BE=x(0≤x≤3),则CE=3-x,根据BF=![]() ,即可得到当x=
,即可得到当x=![]() 时,BF存在最大值
时,BF存在最大值![]() ;
;
(3)连接FH,取EF的中点M,连接BM,HM,依据BM=EM=HM=FM,可得点B,E,H,F四点共圆,连接BH,则∠HBE=∠EFH=30°,进而得到点H在以点B为端点,BC上方且与射线BC夹角为30°的射线上,再过C作CH'⊥BH于点H',根据点E从点B出发,沿BC边运动到点C,即可得到点H从点B沿BH运动到点H',再利用在Rt△BH'C中,BH'=BCcos∠CBH'=3×![]() =
=![]() ,即可得出点H所经过的路径长是
,即可得出点H所经过的路径长是![]() .
.
详解:![]() 证明:如图1,在矩形ABCD中,
证明:如图1,在矩形ABCD中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 由
由![]() 可得,
可得,![]() ,
,![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
在矩形ABCD中,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 当
当![]() 时,BF存在最大值
时,BF存在最大值![]() ;
;
![]() 如图2,连接FH,取EF的中点M,连接BM,HM,
如图2,连接FH,取EF的中点M,连接BM,HM,
在等边三角形EFG中,![]() ,H是EG的中点,
,H是EG的中点,
![]() ,
,![]() ,
,
又![]() 是EF的中点,
是EF的中点,
![]() ,
,
在![]() 中,
中,![]() ,M是EF的中点,
,M是EF的中点,
![]() ,
,
![]() ,
,
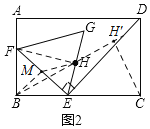
![]() 点B,E,H,F四点共圆,
点B,E,H,F四点共圆,
连接BH,则![]() ,
,
![]() 点H在以点B为端点,BC上方且与射线BC夹角为
点H在以点B为端点,BC上方且与射线BC夹角为![]() 的射线上,
的射线上,
如图,过C作CH'⊥BH于点H',
∵点E从点B出发,沿BC边运动到点C,
∴点H从点B沿BH运动到点H',
在Rt△BH'C中,∠BH'C=90°,
∴BH'=BCcos∠CBH'=3×![]() =
=![]() ,
,
![]() 点H所经过的路径长是
点H所经过的路径长是![]() .
.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市民一户一表"生活用水阶梯式计费价格表的部分信息:
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
|
|
|
超过 |
|
|
超过 |
|
|
(说明:每户生产的污水量等于该户自来水用量;②水费=自来水费用+污水处理费)
已知小王家2018年7月用水![]() 吨,交水费
吨,交水费![]() 元.8月份用水
元.8月份用水![]() 吨,交水费
吨,交水费![]() 元.
元.
(1)求![]() 的值;
的值;
(2)如果小王家9月份上交水费![]() 元,则小王家这个月用水多少吨?
元,则小王家这个月用水多少吨?
(3)小王家10月份忘记了去交水费,当他11月去交水费时发现两个月一共用水50吨,其中10月份用水超过![]() 吨,一共交水费
吨,一共交水费![]() 元,其中包含
元,其中包含![]() 元滞纳金,求小王家11月份用水多少吨? (滞纳金:因未能按期缴纳水费,逾期要缴纳的“罚款金额”)
元滞纳金,求小王家11月份用水多少吨? (滞纳金:因未能按期缴纳水费,逾期要缴纳的“罚款金额”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知点A(﹣2,4),B(﹣5,4),C(﹣3,1),直线l经过点(1,0),且与y轴平行.
(1)请在图中画出△ABC;
(2)若△A1B1C1与△ABC关于直线l对称.请在图中画出△A1B1C1;
(3)若点P(a,b)关于直线l的对称点为P1,则点P1的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
(探究与发现)
如图1,在数轴上点![]() 表示的数是8,点
表示的数是8,点![]() 表示的数是4,求线段
表示的数是4,求线段![]() 的中点
的中点![]() 所示的数对于求中点表示数的问题,只要用点
所示的数对于求中点表示数的问题,只要用点![]() 所表示的数-8,加上点
所表示的数-8,加上点![]() 所表示的数4,得到的结果再除以2,就可以得到中点
所表示的数4,得到的结果再除以2,就可以得到中点![]() 所表示的数:即
所表示的数:即![]() 点表示的数为:
点表示的数为:![]() .
.
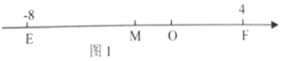
(理解与应用)
把一条数轴在数![]() 处对折,使表示-20和2020两数的点恰好互相重合,则
处对折,使表示-20和2020两数的点恰好互相重合,则![]() .
.
(拓展与延伸)
如图2,已知数轴上有![]() 、
、![]() 、
、![]() 三点,点
三点,点![]() 表示的数是-6,点
表示的数是-6,点![]() 表示的数是8.
表示的数是8.![]() .
.
(1)若点![]() 以每秒3个单位的速度向右运动,点
以每秒3个单位的速度向右运动,点![]() 同时以每秒1个单位的速度向左运动设运动时间为
同时以每秒1个单位的速度向左运动设运动时间为![]() 秒.
秒.
①点![]() 运动
运动![]() 秒后,它在数轴上表示的数表示为 (用含
秒后,它在数轴上表示的数表示为 (用含![]() 的代数式表示)
的代数式表示)
②当点![]() 为线段
为线段![]() 的中点时,求
的中点时,求![]() 的值.
的值.
(2)若(1)中点![]() 、点
、点![]() 的运动速度、运动方向不变,点
的运动速度、运动方向不变,点![]() 从原点以每秒2个单位的速度向右运动,假设
从原点以每秒2个单位的速度向右运动,假设![]() 、
、![]() 、
、![]() 三点同时运动,求多长时间点
三点同时运动,求多长时间点![]() 到点
到点![]() 的距离相等?
的距离相等?

查看答案和解析>>
科目:初中数学 来源: 题型:
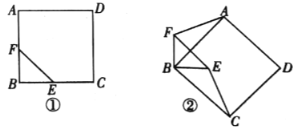
【题目】如图①,已知四边形![]() 是正方形点
是正方形点![]() 分别在边
分别在边![]() 上,且
上,且![]() 是等腰直角三角形
是等腰直角三角形
![]() 此时
此时![]() 与
与![]() 有怎样的数关系和位关系?请直接写出结论,不用证明
有怎样的数关系和位关系?请直接写出结论,不用证明
![]() 如图②,正方形
如图②,正方形![]() 绕点
绕点![]() 顺时针旋转一个锐角后,连接
顺时针旋转一个锐角后,连接![]() ,此时
,此时![]() 与
与![]() 仍有
仍有![]() 中的关系吗?如果成立,请说明理由.否则,请举出反例;
中的关系吗?如果成立,请说明理由.否则,请举出反例;
![]() 将正方形
将正方形![]() 由图①的位置开始,绕点
由图①的位置开始,绕点![]() 顺时针旋转一周,在旋转的过程中,当点
顺时针旋转一周,在旋转的过程中,当点![]() 和点
和点![]() 之间的距离达到最小和最大时,旋转的角度分别是多少?请直接 写出结果.
之间的距离达到最小和最大时,旋转的角度分别是多少?请直接 写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有五张形状、大小、质地都相同的卡片,这些卡片上面分别画有下列图形:①正方形;②等边三角形;③平行四边形;④等腰三角形;⑤圆.将卡片背面朝上洗匀,从中随机抽取一张,抽出的纸片正面图形是轴对称图形,但不是中心对称图形的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位:元) | 18 | 12 |
备注 | 1.用不超过16800元购进A,B两类图书共1000本; 2.A类图书不少于600本; …… |
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A,B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△DAC 和△EBC 均是等边三角形,A,C,B 三点在一条直线上,AE,BD 分别与 CD、CE 交于点 M、N,AE,BD 相交于点 O.
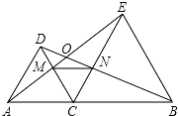
(1)求证:△ACE ≌△DCB;
(2)求∠AOD 的度数
(3)判断△CMN 的形状并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com