
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 受国际炒家炒作的影响,今年棉花价格出现了大幅度波动,1至3月份,棉价大幅度上涨,其价格y1(元/吨)与月份x之间的函数关系式:y1=2200x+24200(1≤x≤3,且x取整数).而从4月份起,棉价大幅度走低,其价格y2(元/吨)与月份x(4≤x≤6,且x取整数)之间的函数关系如图所示.
受国际炒家炒作的影响,今年棉花价格出现了大幅度波动,1至3月份,棉价大幅度上涨,其价格y1(元/吨)与月份x之间的函数关系式:y1=2200x+24200(1≤x≤3,且x取整数).而从4月份起,棉价大幅度走低,其价格y2(元/吨)与月份x(4≤x≤6,且x取整数)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
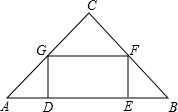 如图,在直角△ABC中,∠C=90°,矩形DEFG的四个顶点都在△ABC的边上,已知:AC=4,BC=3.
如图,在直角△ABC中,∠C=90°,矩形DEFG的四个顶点都在△ABC的边上,已知:AC=4,BC=3.查看答案和解析>>
科目:初中数学 来源: 题型:
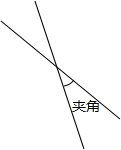 两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的“夹角”(见图)现在平面上有若干条直线,它们两两相交并且“夹角”只能是30°或者是60°或者是90°时,问:平面上最多有多少条直线?当直线条数最多时,所有的“夹角”的和是多少?
两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的“夹角”(见图)现在平面上有若干条直线,它们两两相交并且“夹角”只能是30°或者是60°或者是90°时,问:平面上最多有多少条直线?当直线条数最多时,所有的“夹角”的和是多少?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
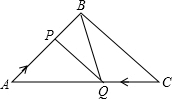 如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向A点运动,设运动时间为x秒.
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向A点运动,设运动时间为x秒.| S△BCQ |
| S△ABC |
| 1 |
| 3 |
| S△APQ |
| S△ABQ |
查看答案和解析>>
科目:初中数学 来源: 题型:
 正方形ABCD边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.
正方形ABCD边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com