

分析 (1)若证AB平分∠MAN,可证∠FAB=∠NAB,根据题意FC垂直平分AB可得∠FAB=∠FBA,又∠GBA=∠GNA=∠NAB,可得∠FAB=∠NAB;
(2)仍然平分,需证∠FAB=∠NAB,而∠NAB=∠NGB,由图可知∠NGB=∠BFE+∠FEG、∠FAB=∠BAG+∠FAG,显然∠BAG=∠BFE,现在需证∠FAG=∠FEG,这可以由∠AGF=∠AEF=90°知A、E、G、F四点在同一个圆上可得;
(3)由(2)知AB平分∠MAN,求AN的长可转化为求AM,显然Rt△ABM∽Rt△AFE可得AM=$\frac{AB•AE}{AF}$,RT△OCE中可求OE长,进而在RT△AEF中可求出AF的长即可.
解答 解:(1)∵CD⊥OB,且OA=OB,
∴FA=FB,
∴∠FAB=∠FBA,
又∵$\widehat{AG}$所对得圆周角∠GBA=∠GNA,
∴∠FAB=∠GNA,
∵OA=ON,
∴∠GNA=∠NAB,
∴∠FAB=∠NAB,即AB平分∠MAN;
(2)如图,连接AG,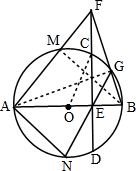
则∠AGF=∠AEF=90°,
∴AF的中点到A、E、G、F四点的距离相等,即A、E、G、F四点在同一个圆上.
∴弦FG所对的圆周角∠FAG=∠FEG.
∵∠BAG+∠ABG=∠BFE+∠FBE=90°,
∴∠BAG=∠BFE.
∵∠BGN=∠BFE+∠FEG,而∠BAM=∠FAG+∠BAG,
∴∠MAB=∠NGB.
∵∠NGB=∠NAB,
∴∠MAB=∠NAB.
∴AB平分∠MAN.
(3)连接OC、BM,
∵OC=5,CE=3,
∴在Rt△OEC中得OE=4.
∴AE=9.
在Rt△AEF,EF=6,
∴AF=3$\sqrt{13}$.
∵AB=10,由Rt△ABM∽Rt△AFE得$\frac{AM}{AE}=\frac{AB}{AF}$,
∴AM=$\frac{AB•AE}{AF}$=$\frac{30\sqrt{13}}{13}$.
∵AB平分∠MAN,
∴AN=AM=$\frac{30\sqrt{13}}{13}$.
点评 本题主要考查有关圆的综合知识,对圆中的相关定理的掌握及利用有关定理、性质进行角度间的转换比较关键.


科目:初中数学 来源: 题型:解答题
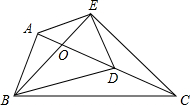 如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的三角板如图放置,使三角板斜边的两个端点分别与A、D重合,E为直角顶点,连接EC、BE.
如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的三角板如图放置,使三角板斜边的两个端点分别与A、D重合,E为直角顶点,连接EC、BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
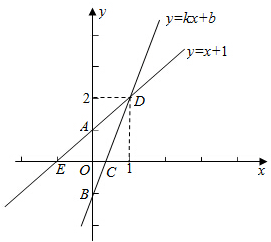 如图,已知直线y=x+1与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),并且与x轴以及直线y=x+1分别交于点C、D.
如图,已知直线y=x+1与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),并且与x轴以及直线y=x+1分别交于点C、D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “十字相乘法”能把二次三项式分解因式,对于形如ax2+bxy+cy2的x,y二次三项式来说,方法的关键是把x2项系数a分解成两个因数a1,a2的积,即a=a1•a2,把y2项系数c分解成两个因数,c1,c2的积,即c=c1•c2,并使a1•c2+a2•c1正好等于xy项的系数b,那么可以直接写成结果:ax2+bxy+cy2=(a1x+c1y)(a2x+c2y)
“十字相乘法”能把二次三项式分解因式,对于形如ax2+bxy+cy2的x,y二次三项式来说,方法的关键是把x2项系数a分解成两个因数a1,a2的积,即a=a1•a2,把y2项系数c分解成两个因数,c1,c2的积,即c=c1•c2,并使a1•c2+a2•c1正好等于xy项的系数b,那么可以直接写成结果:ax2+bxy+cy2=(a1x+c1y)(a2x+c2y)
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-(x+3)2+1 | B. | y=-(x+1)2+3 | C. | y=-(x-1)2+4 | D. | y=-(x+1)2+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中有一个正方形OACB,点A坐标为(4,0),M、N分别是OA、AC上的两个动点,当M点在OA上运动时,一直保持BM和MN垂直.
在平面直角坐标系中有一个正方形OACB,点A坐标为(4,0),M、N分别是OA、AC上的两个动点,当M点在OA上运动时,一直保持BM和MN垂直.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com