
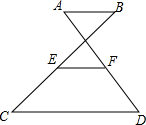
 如图,AB∥CD,点E是BC的中点,点F是AD的中点,若AB=5,CD=12,求EF的长.
如图,AB∥CD,点E是BC的中点,点F是AD的中点,若AB=5,CD=12,求EF的长. 分析 连接AE并延长交CD于点G,可得△AEB≌△CEG,故AE=GE,进而得出EF是△AGD的中位线,再由三角形中位线定理即可得出结论.
解答 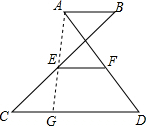 解:连接AE并延长交CD于点G.
解:连接AE并延长交CD于点G.
∵AB∥CD,
∴∠B=∠C;
在△AEB与△CEG中,
∵$\left\{\begin{array}{l}∠B=∠C\\ BE=CE\\∠AEB=∠CEG\end{array}\right.$,
∴△AEB≌△CEG(ASA);
∴AE=EG.
又∵AF=FD,
∴EF∥GD,EF=$\frac{1}{2}$GD,即EF是△AGD的中位线,
∵AB=CG=5,CD=12,
∴GD=12-5=7,
∴EF=$\frac{1}{2}$GD=$\frac{7}{2}$.
点评 本题主要考查了三角形中位线定理、全等三角形的判定及性质以及平行线的判定问题,根据题意作出辅助线,构造出全全等三角形是解答此题的关键.


科目:初中数学 来源: 题型:选择题
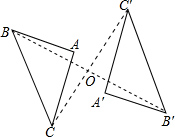 如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )
如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )| A. | ∠ABC=∠A′B′C′ | B. | ∠BOC=∠B′A′C′ | C. | AB=A′B′ | D. | OA=OA′ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
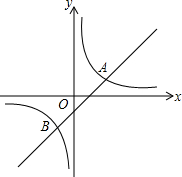 如图,直线y=x+b和双曲线$y=\frac{k}{x}$相交于点A、B,且点A坐标为(2,1)
如图,直线y=x+b和双曲线$y=\frac{k}{x}$相交于点A、B,且点A坐标为(2,1)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
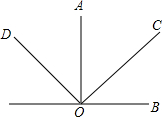 如图,OA⊥OB,OC⊥OD,∠AOC=α,那么∠B0D等于( )
如图,OA⊥OB,OC⊥OD,∠AOC=α,那么∠B0D等于( )| A. | 180°-2α | B. | 180°-α | C. | 90°+$\frac{1}{2}$α | D. | 2α-90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
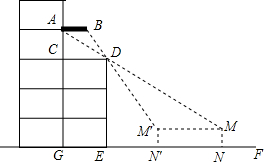 周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳篷的宽度.如图,由于无法直接测量,小凯便在楼前地面上选择了一条直线EF,通过在直线EF上选点观侧,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳篷A点处;当他位于N′点时,视线从M′点通过D点正好落在遮阳篷B点处,这样观测到的两个点A、B间的距离即为遮阳篷的宽.已知AB∥CD∥EF,点C在AG上,AG、DE、MN、M′N′均垂直于EF,MN=M′N′,露台的宽CD=GE.测得CE=5米,EN=12.3米,NN′=6.2米.请你根据以上信息,求出遮阳篷的宽AB是多少米?(结果精确到0.01米)
周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳篷的宽度.如图,由于无法直接测量,小凯便在楼前地面上选择了一条直线EF,通过在直线EF上选点观侧,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳篷A点处;当他位于N′点时,视线从M′点通过D点正好落在遮阳篷B点处,这样观测到的两个点A、B间的距离即为遮阳篷的宽.已知AB∥CD∥EF,点C在AG上,AG、DE、MN、M′N′均垂直于EF,MN=M′N′,露台的宽CD=GE.测得CE=5米,EN=12.3米,NN′=6.2米.请你根据以上信息,求出遮阳篷的宽AB是多少米?(结果精确到0.01米)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 抛物线 | 开口方向 | 对称轴 | 顶点坐标 |
| y=x2-4x+1 | 向上 | x=2 | (2,-3) |
| y=-5(x+2)(x-4) | 向下 | x=1 | (1,45) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3种 | B. | 4种 | C. | 5种 | D. | 6种 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
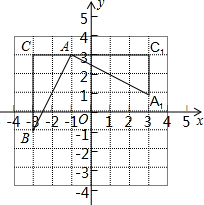 如图,在平面直角坐标系中,A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.
如图,在平面直角坐标系中,A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com