Question

3．在平面直角坐标系xOy中，以O、A、C、B为顶点的四边形是菱形，若点A的坐标是（3，4），点B在x轴的正半轴上，则点C的坐标是（8，4），（3，-4），（-$\frac{7}{6}$，4）．

Answer 1

分析 首先根据题意作出图形，然后分别从四边形OACB、OABC、OCAB是菱形去分析求解即可求得答案．

解答 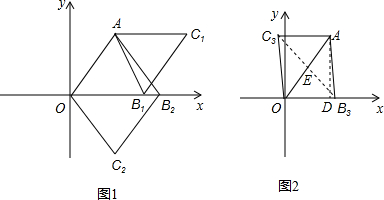解：∵点A的坐标是（3，4），
∴OA=$\sqrt{{3}^{2}+{4}^{2}}$=5，
如图1，若四边形OACB是菱形，则AC∥OB，AC=OB=OA=5，
∴点C₁的坐标为：（8，4）；
若四边形OABC是菱形，
则点C₂的坐标为：（3，-4）；
如图2，若四边形OCAB是菱形，连接BC，过点A作AD⊥OB于点D，
则OE=$\frac{1}{2}$OA=$\frac{5}{2}$，BC⊥OA，
∴∠OEB=∠ODA=90°，∠EOD=∠AOD，
∴△OBE∽△OAD，
∴$\frac{OB}{OA}=\frac{OE}{OD}$，
∴$\frac{OB}{5}=\frac{\frac{5}{2}}{3}$，
解得：OB=$\frac{25}{6}$，
∴点C₃的坐标为：（-（$\frac{25}{6}$-3），4），
即（-$\frac{7}{6}$，4）．
综上所述，点C的坐标为：（8，4），（3，-4），（-$\frac{7}{6}$，4）．
故答案为：（8，4），（3，-4），（-$\frac{7}{6}$，4）．

点评 此题考查了菱形的性质以及勾股定理．注意分类讨论思想的应用．