
分析 (1)直接利用十字相乘法把方程左边进行因式分解得到(3x-1)(x+3)=0,再解两个一元一次方程即可;
(2)首先去分母得到7x-7+3x+3=6x,求出x的值,再进行验根.
解答 解:(1)∵3x2+8x-3=0,
∴(3x-1)(x+3)=0,
∴3x-1=0或x+3=0,
∴x1=$\frac{1}{3}$,x2=-3;
(2)∵$\frac{7}{{x}^{2}+x}$+$\frac{3}{{x}^{2}-x}$=$\frac{6}{{x}^{2}-1}$,
∴$\frac{7(x-1)}{x(x+1)(x-1)}$+$\frac{3(x+1)}{x(x+1)(x-1)}$=$\frac{6x}{x(x+1)(x-1)}$,
∴7x-7+3x+3=6x,
∴4x=4,
∴x=1,
经检验x=1时原方程不成立,
所以此方程无解.
点评 本题主要考查了因式分解法解一元二次方程以及解分式方程的知识,解答本题的关键是掌握因式分解法解方程的步骤以及注意解分式方程要验根,此题难度不大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
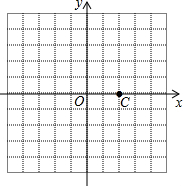 已知:抛物线C1:y=(x+1)2+1
已知:抛物线C1:y=(x+1)2+1查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知一次函数y=-$\frac{1}{2}$x+2的图象分别交x轴,y轴于B点、A点,抛物线y=ax2+$\frac{1}{2}$x+c的图象经过A、B两点,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
如图,已知一次函数y=-$\frac{1}{2}$x+2的图象分别交x轴,y轴于B点、A点,抛物线y=ax2+$\frac{1}{2}$x+c的图象经过A、B两点,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≠2 | B. | x≥3 | C. | x>3且x≠2 | D. | x≥3且x≠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com