
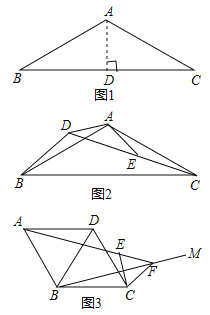
ΓΨΧβΡΩΓΩ»γΆΦΘΚ
(1)Θ®Έ Χβ±≥ΨΑΘ©»γΆΦ1Θ§Β»―ϋΓςABCΘ§AB=AC,ΓœBAC=120ΓψΘ§‘ρ![]() =________.
=________.
(2)Θ®«®“Τ”Π”ΟΘ©»γΆΦ2Θ§ΓςABCΚΆΓςABEΕΦ «Β»―ϋ»ΐΫ«–ΈΘ§ΓœBAC=ΓœDAE=120Γψ,D,E,C»ΐΒψ‘ΎΆ§-Χθ÷±œΏ…œΘ§Ν§ΫαBDΘ°«σœΏΕΈADΘ§BDΘ§CD÷°ΦδΒΡ ΐΝΩΙΊœΒ ΫΘΜ
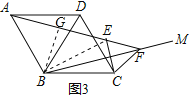
(3)Θ®ΆΊ’Ι―”…λΘ©»γΆΦ3Θ§‘ΎΝβ–ΈABCD÷–Θ§ΓœABC=120ΓψΘ§‘ΎΓœABCΡΎΉς…δœΏBMΘ§ΉςΒψCΙΊ”ΎBMΒΡΕ‘≥ΤΒψEΘ§Ν§ΫαAE≤Δ―”≥ΛΫΜBM”ΎΒψFΘ§Ν§ΫαCE, CFΘ°»τAE=4Θ§CE=1Θ°«σBFΒΡ≥Λ.
ΓΨ¥πΑΗΓΩ(1)![]() ΘΜ(2)CD=
ΘΜ(2)CD=![]() AD+BDΘΜ(3)2
AD+BDΘΜ(3)2![]() .
.
ΓΨΫβΈωΓΩ
Έ Χβ±≥ΨΑΘΚΉςADΓΆBC”ΎDΘ§ΗυΨίΒ»―ϋ»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫBD=CDΘ§ΗυΨί»ΐΫ«–ΈΡΎΫ«ΚΆΕ®άμ«σ≥ωΓœABCΘ§ΗυΨί”ύœ“ΒΡΕ®“εΦΤΥψΦ¥Ω…ΘΜ
«®“Τ”Π”ΟΘΚ÷ΛΟςΓςDABΓ’ΓςEACΘ§ΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫBD=CEΘ§”…Έ Χβ±≥ΨΑΒΟΒΫCDΓΔADΓΔBDΒΡΙΊœΒΘΜ
ΆΊ’Ι―”…λΘΚΉςBGΓΆAE”ΎGΘ§Ν§Ϋ”BEΘ°”…BM¥Ι÷±ΤΫΖ÷CEΘ§Ω…ΒΟΓœEBF=ΓœCBFΘ§‘ΌΗυΨίAB=BEΘ§BGΓΆAEΘ§Ω…ΒΟΓœABG=ΓœEBGΘ§ΫχΕχΒΟ≥ωΓœGBF=![]() ΓœABC=60ΓψΘ§‘ΎΥΡ±Ώ–ΈBCEG÷–Θ§«σΒΟΓœCEG=120ΓψΘ§ΒΟΒΫΓœCEF=60ΓψΘ§“άΨίFE=FCΘ§ΒΟΒΫΓςEFC «Β»±Ώ»ΐΫ«–ΈΘ§”…AE=4Θ§EC=EF=1Θ§Ω…ΒΟAG=GE=2Θ§FG=3Θ§‘ΌΗυΨί‘ΎRtΓςBGF÷–Θ§ΓœBFG=30ΓψΘ§Φ¥Ω…ΒΟΒΫBFΘ°
ΓœABC=60ΓψΘ§‘ΎΥΡ±Ώ–ΈBCEG÷–Θ§«σΒΟΓœCEG=120ΓψΘ§ΒΟΒΫΓœCEF=60ΓψΘ§“άΨίFE=FCΘ§ΒΟΒΫΓςEFC «Β»±Ώ»ΐΫ«–ΈΘ§”…AE=4Θ§EC=EF=1Θ§Ω…ΒΟAG=GE=2Θ§FG=3Θ§‘ΌΗυΨί‘ΎRtΓςBGF÷–Θ§ΓœBFG=30ΓψΘ§Φ¥Ω…ΒΟΒΫBFΘ°
Έ Χβ±≥ΨΑΘΚ»γΆΦ1Θ§ΉςADΓΆBC”ΎDΘ§
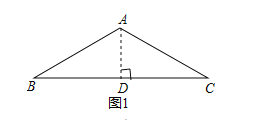
ΓΏAB=ACΘ§ΓœBAC=120ΓψΘ§
ΓύBD=CDΘ§ΓœABC=30ΓψΘ§
cosB=![]() Θ§Φ¥
Θ§Φ¥![]() Θ§
Θ§
ΓύBC=![]() ABΘ§Φ¥
ABȧ֥![]() ȧ
Θ§
Ι ¥πΑΗΈΣ![]() ΘΜ
ΘΜ
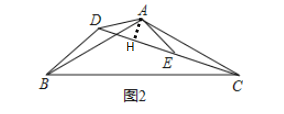
«®“Τ”Π”ΟΘΚ»γΆΦ2Θ§ΓΏΓœBAC=ΓœDAEΘ§
ΓύΓœDAB=ΓœEACΘ§
‘ΎΓςDABΚΆΓςEAC÷–Θ§
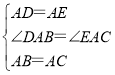 Θ§
Θ§
ΓύΓςDABΓ’ΓςEACΘ®SASΘ©Θ§
ΓύBD=CEΘ§
”…Έ Χβ±≥ΨΑΩ…÷ΣΘ§DE=![]() ADΘ§
ADȧ
ΓύCD=DE+EC=![]() AD+BDΘΜ
AD+BDΘΜ
ΆΊ’Ι―”…λΘΚ÷ΛΟςΘΚ»γΆΦ3Θ§ΉςBGΓΆAE”ΎGΘ§Ν§Ϋ”BEΘ§
ΓΏEΓΔCΙΊ”ΎBMΕ‘≥ΤΘ§
ΓύBC=BEΘ§FE=FCΘ§BFΓΆCEΘ§
ΓύΓœEBF=ΓœCBFΘ§
ΓΏ‘ΎΝβ–ΈABCD÷–Θ§AB=BCΘ§ΓœABC=120ΓψΘ§
ΓύAB=BEΘ§”÷BGΓΆAEΘ§
ΓύΓœABG=ΓœEBGΘ§
ΓύΓœEBG+ΓœEBF=![]() ΓœABC=60ΓψΘ§
ΓœABC=60ΓψΘ§
ΓύΥΡ±Ώ–ΈBNEG÷–Θ§ΓœCEG=360Γψ-90Γψ-90Γψ-60Γψ=120ΓψΘ§
ΓύΓœCEF=60ΓψΘ§”÷FE=FCΘ§
ΓύΓςEFC «Β»±Ώ»ΐΫ«–ΈΘ§
ΓΏAE=4Θ§EC=EF=1Θ§
ΓύAG=GE=2Θ§FG=3Θ§
‘ΎRtΓςBGF÷–Θ§ΓœBFG=30ΓψΘ§
ΓύBF=![]() =2
=2![]() Θ°
Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΚ÷Σ:»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§÷±œΏ
÷–Θ§÷±œΏ![]() ”κ
”κ![]() ÷αΓΔ
÷αΓΔ![]() ÷αΖ÷±πΫΜ”Ύ
÷αΖ÷±πΫΜ”Ύ![]() ΝΫΒψΘ§
ΝΫΒψΘ§![]() «÷±œΏ
«÷±œΏ![]() …œ“ΜΕ·ΒψΘ§Γ―
…œ“ΜΕ·ΒψΘ§Γ―![]() ΒΡΑκΨΕΈΣ2Θ°
ΒΡΑκΨΕΈΣ2Θ°
Θ®1Θ©≈–Εœ‘≠Βψ![]() ”κΓ―
”κΓ―![]() ΒΡΈΜ÷ΟΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
ΒΡΈΜ÷ΟΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®2Θ©Β±Γ―![]() ”κ
”κ![]() ÷αœύ«– ±Θ§«σ≥ω«–ΒψΒΡΉχ±ξΘ°
÷αœύ«– ±Θ§«σ≥ω«–ΒψΒΡΉχ±ξΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕ®“εΘΚ–Έ»γyΘΫ|G|Θ®GΈΣ”ΟΉ‘±δΝΩ±μ ΨΒΡ¥ζ ΐ ΫΘ©ΒΡΚ· ΐΫ–ΉωΨχΕ‘÷ΒΚ· ΐΘ°
άΐ»γΘ§Κ· ΐyΘΫ|x©¹1|Θ§yΘΫ![]() Θ§yΘΫ|©¹x2+2x+3|ΕΦ «ΨχΕ‘÷ΒΚ· ΐΘ°
Θ§yΘΫ|©¹x2+2x+3|ΕΦ «ΨχΕ‘÷ΒΚ· ΐΘ°
ΨχΕ‘÷ΒΚ· ΐ±Ψ÷ «Ζ÷ΕΈΚ· ΐΘ§άΐ»γΘ§Ω…“‘ΫΪyΘΫ|x|–¥≥…Ζ÷ΕΈΚ· ΐΒΡ–Έ ΫΘΚ![]() Θ°
Θ°
ΧΫΥς≤ΔΫβΨωœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©ΫΪΚ· ΐyΘΫ|x©¹1|–¥≥…Ζ÷ΕΈΚ· ΐΒΡ–Έ ΫΘΜ
Θ®2Θ©»γΆΦ1Θ§Κ· ΐyΘΫ|x©¹1|ΒΡΆΦœσ”κx÷αΫΜ”ΎΒψAΘ®1Θ§0Θ©Θ§”κΚ· ΐyΘΫ![]() ΒΡΆΦœσΫΜ”ΎBΘ§CΝΫΒψΘ§ΙΐΒψBΉςx÷αΒΡΤΫ––œΏΖ÷±πΫΜΚ· ΐyΘΫ
ΒΡΆΦœσΫΜ”ΎBΘ§CΝΫΒψΘ§ΙΐΒψBΉςx÷αΒΡΤΫ––œΏΖ÷±πΫΜΚ· ΐyΘΫ![]() Θ§yΘΫ|x©¹1|ΒΡΆΦœσ”ΎDΘ§EΝΫΒψΘ°«σ÷ΛΓςABEΓΉΓςCDEΘΜ
Θ§yΘΫ|x©¹1|ΒΡΆΦœσ”ΎDΘ§EΝΫΒψΘ°«σ÷ΛΓςABEΓΉΓςCDEΘΜ
Θ®3Θ©“―÷ΣΚ· ΐyΘΫ|©¹x2+2x+3|ΒΡΆΦœσ”κy÷αΫΜ”ΎFΒψΘ§”κx÷αΫΜ”ΎMΘ§NΝΫΒψΘ®ΒψM‘ΎΒψNΒΡΉσ±ΏΘ©Θ§ΒψP‘ΎΚ· ΐyΘΫ|©¹x2+2x+3|ΒΡΆΦœσ…œΘ®ΒψP”κΒψF≤Μ÷ΊΚœΘ©Θ§PHΓΆx÷αΘ§¥ΙΉψΈΣHΘ°»τΓςPMH”κΓςMOFœύΥΤΘ§«κ÷±Ϋ”–¥≥ωΥυ”–ΖϊΚœΧθΦΰΒΡΒψPΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥ¥ΌΫχ―ß…ζΕύ―υΜ·ΖΔ’ΙΘ§Ρ≥–ΘΉι÷·ΩΣ’ΙΝΥ…γΆ≈ΜνΕ·Θ§Ζ÷±π…η÷ΟΝΥΧε”ΐάύΓΔ“’ θάύΓΔΈΡ―ßάύΦΑΤδΥϋάύ…γΆ≈Θ®“Σ«σ»Υ»Υ≤Έ”κ…γΆ≈Θ§ΟΩ»Υ÷ΜΡή―Γ‘ώ“ΜœνΘ©Θ°ΈΣΝΥΫβ―ß…ζœ≤Α°ΡΡ÷÷…γΆ≈ΜνΕ·Θ§―ß–ΘΉωΝΥ“Μ¥Έ≥ι―υΒς≤ιΘ°ΗυΨί ’Φ·ΒΫΒΡ ΐΨίΘ§Μφ÷Τ≥…»γœ¬ΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ§«κΗυΨίΆΦ÷–ΧαΙ©ΒΡ–≈œΔΘ§Άξ≥…œ¬Ν–Έ ΧβΘΚ
Θ®1Θ©¥Υ¥ΈΙ≤Βς≤ιΝΥΕύ…Ό»ΥΘΩ
Θ®2Θ©«σΧε”ΐ…γΆ≈‘Ύ…»–ΈΆ≥ΦΤΆΦ÷–Υυ’Φ‘≤–ΡΫ«ΒΡΕ» ΐΘΜ
Θ®3Θ©«κΫΪΧθ–ΈΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
Θ®4Θ©»τΗΟ–Θ”–3000Οϊ―ß…ζΘ§«κΙάΦΤœ≤ΜΕΈΡ―ßάύ…γΆ≈ΒΡ―ß…ζ”–Εύ…Ό»ΥΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
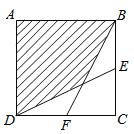
ΓΨΧβΡΩΓΩ»γΆΦΘ§’ΐΖΫ–ΈABCDΒΡ±Ώ≥ΛΈΣ4cmΘ§ΒψEΘ§FΖ÷±π «BCΘ§CDΒΡ÷–ΒψΘ§Ν§ΫαBFΘ§DEΘ§‘ρΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐ «________cm2.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ÷–ΜΣΈΡΟςΘ§‘¥‘ΕΝς≥ΛΘΜ÷–ΜΣΚΚΉ÷Θ§‘Δ“β…νΙψΘ°ΈΣΝΥ¥Ϊ≥–÷–ΜΣΟώΉε”≈–ψ¥ΪΆ≥ΈΡΜ·Θ§Έ“ –Ρ≥÷–―ßΨΌ––ΓΑΚΚΉ÷Χΐ–¥Γ±±»»ϋΘ§»ϋΚσ’ϊάμ≤Έ»ϋ―ß…ζΒΡ≥…Φ®Θ§ΫΪ―ß…ζΒΡ≥…Φ®Ζ÷ΈΣAΘ§BΘ§CΘ§DΥΡΗωΒ»ΦΕΘ§≤ΔΫΪΫαΙϊΜφ÷Τ≥…»γΆΦΥυ ΨΒΡΧθ–ΈΆ≥ΦΤΆΦΚΆ…»–ΈΆ≥ΦΤΆΦΘ§ΒΪΨυ≤ΜΆξ’ϊΘ°

«κΡψΗυΨίΆ≥ΦΤΆΦΫβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©≤ΈΦ”±»»ϋΒΡ―ß…ζΙ≤”–____ΟϊΘΜ
Θ®2Θ©‘Ύ…»–ΈΆ≥ΦΤΆΦ÷–Θ§mΒΡ÷ΒΈΣ____Θ§±μ ΨΓΑDΒ»ΦΕΓ±ΒΡ…»–ΈΒΡ‘≤–ΡΫ«ΈΣ____Ε»ΘΜ
Θ®3Θ©ΉιΈ·ΜαΨωΕ®¥”±Ψ¥Έ±»»ϋΜώΒΟAΒ»ΦΕΒΡ―ß…ζ÷–Θ§―Γ≥ω2Οϊ»Ξ≤ΈΦ”»Ϊ –÷–―ß…ζΓΑΚΚΉ÷Χΐ–¥Γ±¥σ»ϋΘ°“―÷ΣAΒ»ΦΕ―ß…ζ÷–Ρ–…ζ”–1ΟϊΘ§«κ”ΟΝ–±μΖ®ΜρΜ≠ ςΉ¥ΆΦΖ®«σ≥ωΥυ―Γ2Οϊ―ß…ζ«ΓΚΟ «“ΜΟϊΡ–…ζΚΆ“ΜΟϊ≈°…ζΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ–ΓœΡΆ§―ߥ”Φ“ΒΫ―ß–Θ”–![]() Θ§
Θ§![]() ΝΫΧθ≤ΜΆ§ΒΡΙΪΫΜœΏ¬ΖΘ°ΈΣΝΥΫβ‘γΗΏΖεΤΎΦδ’β»ΐΧθœΏ¬Ζ…œΒΡΙΪΫΜ≥Β¥”ΦΉΒΊΒΫ““ΒΊΒΡ”Ο ±«ιΩωΘ§‘ΎΟΩΧθœΏ¬Ζ…œΥφΜζ―Γ»ΓΝΥ500ΗωΑύ¥ΈΒΡΙΪΫΜ≥ΒΘ§ ’Φ·ΝΥ’β–©Αύ¥ΈΒΡΙΪΫΜ≥Β”Ο ±Θ®ΒΞΈΜΘΚΖ÷÷”Θ©ΒΡ ΐΨίΘ§Ά≥ΦΤ»γœ¬ΘΚ
ΝΫΧθ≤ΜΆ§ΒΡΙΪΫΜœΏ¬ΖΘ°ΈΣΝΥΫβ‘γΗΏΖεΤΎΦδ’β»ΐΧθœΏ¬Ζ…œΒΡΙΪΫΜ≥Β¥”ΦΉΒΊΒΫ““ΒΊΒΡ”Ο ±«ιΩωΘ§‘ΎΟΩΧθœΏ¬Ζ…œΥφΜζ―Γ»ΓΝΥ500ΗωΑύ¥ΈΒΡΙΪΫΜ≥ΒΘ§ ’Φ·ΝΥ’β–©Αύ¥ΈΒΡΙΪΫΜ≥Β”Ο ±Θ®ΒΞΈΜΘΚΖ÷÷”Θ©ΒΡ ΐΨίΘ§Ά≥ΦΤ»γœ¬ΘΚ
ΙΪΫΜ≥Β”Ο ± ΤΒ ΐ ΙΪΫΜ≥Β¬ΖœΏ |
|
|
|
| ΉήΦΤ |
| 59 | 151 | 166 | 124 | 500 |
| 43 | 57 | 149 | 251 | 500 |
Ψί¥ΥΙάΦΤΘ§‘γΗΏΖεΤΎΦδΘ§≥ΥΉχ![]() œΏ¬ΖΓΑ”Ο ±≤Μ≥§Ιΐ35Ζ÷÷”Γ±ΒΡΗ≈¬ ΈΣ__________Θ§»τ“Σ‘Ύ40Ζ÷÷”÷°ΡΎΒΫ¥ο―ß–ΘΘ§”ΠΨΓΝΩ―Γ‘ώ≥ΥΉχ__________Θ®Χν
œΏ¬ΖΓΑ”Ο ±≤Μ≥§Ιΐ35Ζ÷÷”Γ±ΒΡΗ≈¬ ΈΣ__________Θ§»τ“Σ‘Ύ40Ζ÷÷”÷°ΡΎΒΫ¥ο―ß–ΘΘ§”ΠΨΓΝΩ―Γ‘ώ≥ΥΉχ__________Θ®Χν![]() Μρ
Μρ![]() Θ©œΏ¬ΖΘ°
Θ©œΏ¬ΖΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
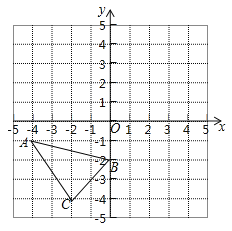
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABCΒΡ»ΐΗωΕΞΒψΕΦ‘Ύ±Ώ≥ΛΈΣ1ΒΡ–Γ’ΐΖΫ–ΈΉι≥…ΒΡΆχΗώΒΡΗώΒψ…œΘ§“‘ΒψOΈΣ‘≠ΒψΫ®ΝΔ÷±Ϋ«Ήχ±ξœΒΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©ΫΪΓςABCœ»œρ…œΤΫ“Τ5ΗωΒΞΈΜΘ§‘Όœρ”“ΤΫ“Τ1ΗωΒΞΈΜΒΟΒΫΓςA1B1C1Θ§Μ≠≥ωΓςA1B1C1Θ§≤Δ÷±Ϋ”–¥≥ωA1ΒΡΉχ±ξΓΓ ΓΓΘΜ
Θ®2Θ©ΫΪΓςA1B1C1»ΤΒψΘ®0Θ§©¹1Θ©Υ≥ ±’κ–ΐΉΣ90ΓψΒΟΒΫΓςA2B2C2Θ§Μ≠≥ωA2B2C2ΘΜ
Θ®3Θ©Ιέ≤λΆΦ–ΈΖΔœ÷Θ§A2B2C2 «”…ΓςABC»ΤΒψΓΓ ΓΓΥ≥ ±’κ–ΐΉΣΓΓ ΓΓΕ»ΒΟΒΫΒΡΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏyΘΫax2ΘΪbxΘΪcΘ®aΓΌ0Θ©ΒΡΕ‘≥Τ÷αΈΣ÷±œΏxΘΫ2Θ§”κx÷αΒΡ“ΜΗωΫΜΒψΉχ±ξΈΣΘ®4Θ§0Θ©Θ§Τδ≤ΩΖ÷ΆΦœσ»γΆΦΥυ ΨΘ§œ¬Ν–Ϋα¬έ’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©
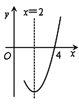
A.Β±xΘΦ2 ±Θ§yΥφx‘ω¥σΕχ‘ω¥σB.aΘ≠bΘΪcΘΦ0
C.£¹ΈοœΏΙΐΒψΘ®Θ≠4Θ§0Θ©D.4aΘΪbΘΫ0
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com