
【题目】如图,将长方形 ABCD 沿 EF 折叠,使点 D 与点 B 重合.
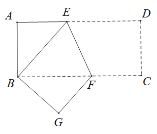
(1)若∠AEB=40°,求∠BFE 的度数;
(2)若 AB=6,AD=18,求 CF 的长.
【答案】(1)70°; (2)8.
【解析】
(1)依据平行线的性质可求得∠BFE=∠FED,然后依据翻折的性质可求得∠BEF=∠DEF,最后根据平角的定义可求得∠BFE的度数;
(2)先依据翻折的性质得到CF=GF,AB=DC=BG=6,然后设CF=GF=x,然后在RT△BGF中,依据勾股定理列出关于x的方程求解即可.
解:(1)∵AD∥BC,
∴∠BFE=∠FED,
由翻折的性质可知:∠BEF=∠DEF,
∴∠BFE=∠FED=∠BEF
∵∠FED+∠BEF+∠AEB=180°
∴2∠BFE =180°-40°=140°,
∴∠BFE=70°;
(2)由翻折的性质可知CF=GF,AB=DC=BG=6,
设CF=GF=x,则BF=18-x,
在Rt△BGF中,依据勾股定理可知:BF2=BG2+GF2,
即(18-x)2=62+x2,
解得:x=8
即CF=8


科目:初中数学 来源: 题型:
【题目】已知y是x的一次函数,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,求:
,求:
(1)这个一次函数的表达式和自变量x的取值范围
(2)当![]() 时,自变量x的值
时,自变量x的值
(3)当![]() 时,自变量x的取值范围.
时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
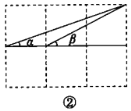
【题目】如图,在由6个大小相同的小正方形组成的方格中,设每个小正方形的边长均为1.
(1)如图①,![]() ,
,![]() ,
,![]() 是三个格点(即小正方形的顶点),判断
是三个格点(即小正方形的顶点),判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;

(2)如图②,连接三格和两格的对角线,求![]() 的度数(要求:画出示意图,并写出证明过程).
的度数(要求:画出示意图,并写出证明过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表


根据以上信息完成下列问题:
(1)直接写出频数分布表中a的值;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC 中,AB、AC 边的垂直平分线相交于点 O,分别交 BC 边于点 M、N,连接 AM,AN.

(1)若△AMN 的周长为 6,求 BC 的长;
(2)若∠MON=30°,求∠MAN 的度数;
(3)若∠MON=45°,BM=3,BC=12,求 MN 的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
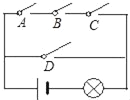
【题目】如图.电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A,B,C都可使小灯泡发光.
(1)任意闭合其中一个开关,则小灯泡发光的概率等于 ;
(2)任意闭合其中两个开关,请用画树状图或列表的方法求出小灯泡发光的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中MN分别在AB、CD上且AM=CN,MN与AC交于点O,连接BO若∠DAC=62°,则∠OBC的度数为( )
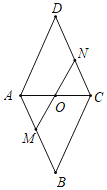
A. 28°B. 52°C. 62°D. 72°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com