
【题目】如图,矩形OABC在平面直角坐标系中,点A在y轴上,点C在![]() 轴上,OC=4,直线
轴上,OC=4,直线![]() 经过点A,交
经过点A,交![]() 轴于点D,点E在线段BC上,ED⊥AD.
轴于点D,点E在线段BC上,ED⊥AD.
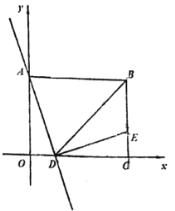
(1)求点E的坐标;
(2)联结BD,求cot∠BDE的值;
(3)点G在直线BC,且∠EDG=45°,求点G的坐标.
【答案】(1)(4,1);(2)2;(3)(4,![]() )或(4,6).
)或(4,6).
【解析】
(1)先求出OA、OD、DC的长度,再证明△AOD≌△DCE,从而得出EC=OD,即可求出E点坐标;(2)作EQ⊥BD,根据等腰三角形的性质可求DQ和EQ的长度,即可求出cot∠BDE;(3)分G在C点下方和B点上方两种情况讨论,借助三角形的相似即可求出相应线段的长,从而求出点的坐标.
(1)∵![]() 经过点A,点A在y轴上,
经过点A,点A在y轴上,
∴A(0,3),即OA=3
当y=0时,![]() ,解得x=1
,解得x=1
∴D(1,0),即OD=1
∵矩形OABC中OC=4,
∴OB=OA=3,DC=OC-OD=3
∠AOC=∠BCD=90°.
∴∠OAD+∠ADO=90°
∵ED⊥AD
∴∠EDC+∠ADO=90°
∴∠EDC=∠OAD
又∵OA=CD=3
∴△AOD≌△DCE(ASA)
∴CE=OD=1
∴E(4,1).
(2)过点E作EQ⊥BD,与BD相交于Q.
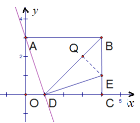
∵DC=BC=3,∠BCD=90°,
∴△BCD为等腰直角三角形,
∴BD=![]() ,∠DBC=45°
,∠DBC=45°
∵EQ⊥BD
∴△EBQ为等腰直角三角形
∵CE=1
∴BE=BC-CE=2
∴BQ=QE=![]()
∴QD=![]()
∴![]()
(3)如图①当G点在C点上方时
∵∠EDG=45°=∠EDC+∠GDC
∠BDC=45°= ∠BDE +∠EDC
∴∠GDC=∠BDE
∴Rt△GCD∽Rt△EQD
∴![]()
即![]()
解得GC=![]()
故G(4,![]() );
);
②当G‘点在B点上方时
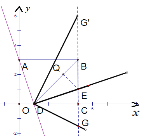
∵∠DG‘C+∠G‘DB=∠DBC=45°
∠G‘DB+∠BDE=∠EDG‘=45°
∴∠DG‘C=∠BDE
∵∠DBC=∠EDG‘ =45°
∴△DEG‘∽△BED
∴![]()
∵![]() ,BE=2,
,BE=2,
∴EG‘=5
∴CG‘=6即G‘(4,6)
故G点坐标为(4,![]() )或(4,6).
)或(4,6).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
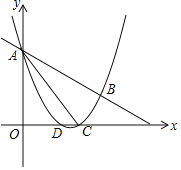
【题目】如图,抛物线![]() 与直线
与直线![]() 交于A,B两点,交x轴与D,C两点,连接AC,已知A(0,3),C(3,0).(1)抛物线的解析式__;(2)设E为线段AC上一点(不含端点),连接DE,一动点M从点D出发,沿线段DE以每秒一个单位速度运动到E点,再沿线段EA以每秒
交于A,B两点,交x轴与D,C两点,连接AC,已知A(0,3),C(3,0).(1)抛物线的解析式__;(2)设E为线段AC上一点(不含端点),连接DE,一动点M从点D出发,沿线段DE以每秒一个单位速度运动到E点,再沿线段EA以每秒![]() 个单位的速度运动到A后停止.若使点M在整个运动中用时最少,则点E的坐标__.
个单位的速度运动到A后停止.若使点M在整个运动中用时最少,则点E的坐标__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于三个数![]() 、
、![]() 、
、![]() ,用
,用![]() 表示这三个数的中位数,用
表示这三个数的中位数,用![]() 表示这三个数中最大数,例如:
表示这三个数中最大数,例如:![]() ,
,![]() ,
,![]() .
.
解决问题:
(1)填空:如果![]() ,则
,则![]() 的取值范围为 ;
的取值范围为 ;
(2)如果![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
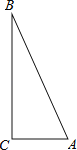
【题目】实践操作
如图,![]() 是直角三角形,
是直角三角形,![]() ,利用直尺和圆规按下列要求作图,并在图中表明相应的字母.(保留作图痕迹,不写作法)
,利用直尺和圆规按下列要求作图,并在图中表明相应的字母.(保留作图痕迹,不写作法)
(1)①作![]() 的平分线,交
的平分线,交![]() 于点
于点![]() ;②以
;②以![]() 为圆心,
为圆心,![]() 为半径作圆.
为半径作圆.
综合运用
在你所作的图中,
(2)![]() 与⊙
与⊙![]() 的位置关系是 ;(直接写出答案)
的位置关系是 ;(直接写出答案)
(3)若![]() ,
,![]() ,求⊙
,求⊙![]() 的半径.
的半径.
(4)在(3)的条件下,求以![]() 为轴把△ABC旋转一周得到的圆锥的侧面积.
为轴把△ABC旋转一周得到的圆锥的侧面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
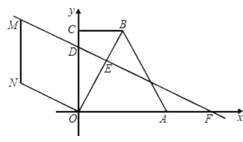
【题目】在直角梯形![]() 中,
中,![]() ,
,![]() ,分别以
,分别以![]() 边所在直线为
边所在直线为![]() 轴,
轴,![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求点![]() 的坐标;
的坐标;
(2)已知![]() 分别为线段
分别为线段![]() 上的点,
上的点,![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点E作EG⊥x轴于G,且EG:OG=2.求直线
,过点E作EG⊥x轴于G,且EG:OG=2.求直线![]() 的解析式;
的解析式;
(3)点![]() 是(2)中直线
是(2)中直线![]() 上的一个动点,在
上的一个动点,在![]() 轴上方的平面内是否存在一点
轴上方的平面内是否存在一点![]() ,使以
,使以![]() 为顶点的四边形为菱形?若存在,请求出
为顶点的四边形为菱形?若存在,请求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8cm,BC=16cm,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
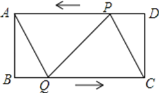
(1)当t为何值时,四边形ABQP是矩形;
(2)当t为何值时,四边形AQCP是菱形;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com