
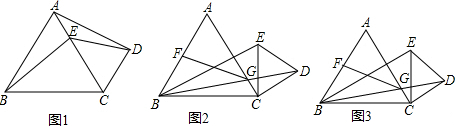
 如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2,∠3=80°,∠A=40°.
如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2,∠3=80°,∠A=40°.分析 (1)由垂直可证明CD∥EF,进一步可证明DG∥BC,可得到∠B=∠ADG;
(2)在△ADG中由三角形内角和定理可求得∠ADG,结合(1)可求得∠B.
解答 (1)证明:∵CD⊥AB,EF⊥AB,
∴∠CDE=∠FEB=90°,
∴CD∥EF,
∴∠2=∠DCB,
∵∠1=∠2,
∴∠1=∠DCB,
∴DG∥BC,
∴∠B=∠ADG;
(2)解:在△ADG中,∠3=80°,∠A=40°,
∴∠ADG=180°-∠A-∠3=180°-80°-40°=60°,
由(1)可知∠B=∠ADG,
∴∠B=60°.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c⇒a∥c.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
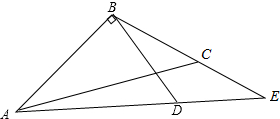 已知,如图,△ABC中,BD⊥AB于点B,AD的延长线交BC于点E.若∠CAE=∠CBD,∠EAB-∠BCA=10°,求出∠BAD的度数.
已知,如图,△ABC中,BD⊥AB于点B,AD的延长线交BC于点E.若∠CAE=∠CBD,∠EAB-∠BCA=10°,求出∠BAD的度数.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
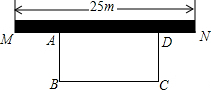 如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在欲砌50m长的墙,砌成一个面积300m2的矩形花园,则BC的长为20 m.
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在欲砌50m长的墙,砌成一个面积300m2的矩形花园,则BC的长为20 m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com